Even in this relatively simple version of the problem, there are a number of details and special cases that come readily to mind: horizontal and vertical line segments, almost horizontal line segments, line segments completely off the paper, line segments partially off the paper, the translation between input and output coordinates, and so on.
Abstraction and algorithm design are crucial to writing correct and efficient geometric algorithms. Abstraction is important because it can organize the details and special cases by order of importance and selectively supress all but a few details at any one time. Algorithm design is important to make sure all the special cases are taken care of at the proper time.
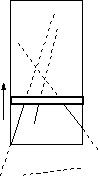
To create a useful set of abstractions, it's helpful to look at a picture of what the program's supposed to be doing:
This picture makes clear what the most important detail is: finding the intersection of the print bar with the line segments to be plotted. These intersections indicate the places where ink should be placed on the paper. Notice how this observation trivializes the special cases involving (parts of) line segments not on the paper: there's no intersection and no ink.
With the central abstraction of line segments intersecting the print bar, the algorithm itself falls readily into place:
for y = y min to y max
for each line segment
if the line segment intersects the line Y = y
plot the intersection points
y min and y max are the smallest and largest line-segment y
coordinates. This algorithm is correct by inspection, and, although there are
a lot of details missing, it's not unreasonable to assert it will meet the
O(Yn) time and O(Y + n) space requirements.
y_min culls any
line segments falling below the start of the paper.
<main()>= (U->)
int main(void) {
pixel y_min, y_max;
lineseg_link * linesegs = read_input(y_min, y_max);
if (linesegs != NULL) {
y_min = max(y_min, 0);
CFLP::advance(y_min);
for (pixel y = y_min; y <= y_max; y++) {
for (lineseg_link * lsl = linesegs; lsl != NULL; lsl = lsl->next)
draw_points(y, lsl->element);
CFLP::advance(1);
}
while (linesegs != NULL) {
delete linesegs->element;
lineseg_link * t = linesegs;
linesegs = linesegs->next;
delete t;
}
}
CFLP::end(true);
return EXIT_SUCCESS;
}
Definesmain(links are to index).
Data Structures
There are two main data structures needed for this program. The first is
something to represent line segments. The line_seg class is a
straightforward implementation of a line segment; the only tricky bit is
possibly ordering the line-segment endpoints so the first coordinate's y value
is no more than the second line segment's y coordinate.
The line segment class is expensive in time and space when compaired to simpler
data structures, such as an array. However, the line segment class is
notationally and conceptually efficient, which is more important that time and
space efficiency at the early stages of program development. Also, note that
almost everyting in the line segment class is constant, which means that
relatively modest C++ compiler should be able to optimize line_seg away to
almost nothing.
<data structures>= (U->) [D->]
class line_seg {
public:
line_seg(pixel xa, pixel ya, pixel xb, pixel yb) :
x1(ya < yb ? xa : xb),
y1(ya < yb ? ya : yb),
x2(ya < yb ? xb : xa),
y2(ya < yb ? yb : ya),
delta_x(static_cast<float>(x2 - x1)),
delta_y(static_cast<float>(y2 - y1))
{
assert(delta_y >= 0);
}
bool is_horizontal(void) const {
return delta_y == 0;
}
bool is_negative_slope(void) const {
return delta_x < 0;
}
bool y_in_segment(pixel y) const {
return (y1 <= y) && (y <= y2);
}
pixel find_x_from_y(pixel y) const {
assert (y_in_segment(y));
assert (!is_horizontal());
return
x1 + static_cast<pixel>((delta_x*static_cast<float>(y - y1))/delta_y);
}
pixel get_max_x(void) const {
return max(x1, x2);
}
pixel get_min_x(void) const {
return min(x1, x2);
}
pixel get_min_y(void) const {
return y1;
}
pixel get_max_y(void) const {
return y2;
}
private:
const pixel x1, y1, x2, y2;
const float delta_x, delta_y;
};
Definesline_seg(links are to index).
The second data structure handles the variable number of line segments are input. Handling a variable number of things using a linked list is relatively simple and efficient.
<data structures>+= (U->) [<-D]
struct lineseg_link {
lineseg_link(line_seg * e, lineseg_link * n = NULL) : element(e), next(n) { }
line_seg * element;
lineseg_link * next;
};
Defineslineseg_link(links are to index).
The Drawing Procedures
Draw the horizontal line pointed to by lsp by setting all the pixels
co-incident with the line.
<draw procedures>= (U->) [D->]
void do_horizontal_line(line_seg * lsp) {
for (pixel x = lsp->get_min_x(); x <= lsp->get_max_x(); x++)
set_pixel(x);
}
Definesdo_horizontal_line(links are to index).
Draw the intersection points between the non-horizontal line pointed to by
lsp and the horizontal line Y = y. The tricky part is dealing
with almost horzontal lines. The problem can be understood by looking at a
picture of an extreme example:
In addition to drawing the intersection point with Y = y, some of the other intermediate pixels between Y = y + 1 (in the case of positive slopes) should also be filled in to prevent the line from becomming to dotty.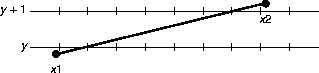
To keep things simple, this code fills in all intermediate pixles to the right
of the intersection point up to but not including the next intersection point
at Y = y + 1 (or Y = y - 1 for negative slopes). next_x is
the intersection coordinate of on the adjacent line.
<draw procedures>+= (U->) [<-D->]
void do_line(line_seg * lsp, pixel y) {
pixel x = lsp->find_x_from_y(y);
pixel next_x = x;
if (lsp->is_negative_slope() && (lsp->get_min_y() < y))
next_x = lsp->find_x_from_y(y - 1);
else if (!lsp->is_negative_slope() && (y < lsp->get_max_y()))
next_x = lsp->find_x_from_y(y + 1);
do set_pixel(x++);
while (x < next_x);
}
Definesdo_line(links are to index).
Draw the intersection points between the line segment pointed to by lsp
with the horizontal line Y = y. If there is no intersection, don't
draw anything.
<draw procedures>+= (U->) [<-D]
static void draw_points(pixel y, line_seg * lsp) {
if (lsp->y_in_segment(y))
if (lsp->is_horizontal())
do_horizontal_line(lsp);
else
do_line(lsp, y);
}
Definesdraw_points(links are to index).
The Read Procedures
Read an input coordinate, translate it to pixel coordinates, and return it in
c. Return true if a coordinate was read, false otherwise.
<read procedures>= (U->) [D->]
static bool read_coord(pixel & c) {
const float iunits_per_inch = 100.0;
const float to_pixels =
static_cast<float>(CFLP::pixels_per_inch)/iunits_per_inch;
int i;
if (!(cin >> i)) return false;
c = static_cast<int>(static_cast<float>(i)*to_pixels + 0.5);
return true;
}
Definesread_coord(links are to index).
Read and return a line segment; return NULL if there's no more line
segments.
<read procedures>+= (U->) [<-D->]
static line_seg * read_lineseg(void) {
pixel x1, y1, x2, y2;
if (!read_coord(x1)) return NULL;
if (!(read_coord(y1) && read_coord(x2) && read_coord(y2))) {
std::cerr << "Unexpected end-of-input in read_lineseg().\n";
exit(EXIT_FAILURE);
}
return new line_seg(x1, y1, x2, y2);
}
Definesread_lineseg(links are to index).
Read the line segments into a linked list; return a pointer to the first
element in the list or NULL if no line segments were read. Also set
y_min and y_max to hold the minimum and maximum y-coordinate values
amoung the line segments read; if no line segments were read, y_min and
y_max are undefined.
<read procedures>+= (U->) [<-D]
static lineseg_link * read_input(pixel & y_min, pixel & y_max) {
lineseg_link * linesegs = NULL;
line_seg * lsp = read_lineseg();
if (lsp == NULL) return linesegs;
linesegs = new lineseg_link(lsp);
y_min = lsp->get_min_y();
y_max = lsp->get_max_y();
while ((lsp = read_lineseg()) != NULL) {
linesegs = new lineseg_link(lsp, linesegs);
y_min = min(y_min, lsp->get_min_y());
y_max = max(y_max, lsp->get_max_y());
}
return linesegs;
}
Definesread_input(links are to index).
The CFLP Interface Procedure
Up to this point, the code has been treating the paper as if it were infinte
(except for the adjustment made to y_min in main()). Now is the time
to recognize the left and right edges of the paper by defining the
set_pixel() interface routine to CFLP::set() that culls pixels too far
to the left or right of the print bar.
<CFLP interface procedures>= (U->)
static inline void set_pixel(pixel x) {
if ((x >= 0) && (static_cast<unsigned>(x) < CFLP::x_extent))
CFLP::set(x);
}
Definesset_pixel(links are to index).
That's it; just a few utility definitions to take care of and the program is complete.
<main.cc>= #include <iostream> #include <cassert> #include <stdlib.h> #include "cflp.h" typedef int pixel; template<typename T> static inline T max(T a, T b) { return a < b ? b : a; } template<typename T> static inline T min(T a, T b) { return a > b ? b : a; } <data structures> <CFLP interface procedures> <draw procedures> <read procedures> <main()>
Definesmain.cc(links are to index).
main()>: D1, U2
main.cc>: D1
This page last modified on 24 February 2001.