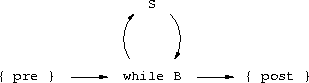Lecture Notes for Concurrent Programming

3 June 2003 - Computations, States, and Predicates

Outline

• Understanding Computations

• States and Histories

• Describing Histories

• Predicate Logic

  • Predicate Operators

  • Forall Predicates

  • Forsome Predicates

  • State Predicates

• A Programming Logic

  • Procedure Pre- and Post-conditions

  • Assignment Statements

  • Statement Sequences

  • If Statements

  • While Statements

  • Weakening and Strengthening

Understanding Computations

• Given a computation, how do you understand what it does?

• Run the computation and analyze it.

  • Known as post-mortem or analysis via debugging.

• Play computer and execute it on paper.

  • Useful for learning the computation's structure.

  • Humans don't make good computers.

• Understand how the state are transformed.

  • Computations, after all, manipulate state.

States and Histories

• A computation's state is the data on which it works.

  • Internal (variables), external (files), and hidden (program counter).

• A state instance is the values of all state between any two statements.

  • State doesn't change between statements.

  • Usually only a subset of the state is of interest.

  • The initial state instance before the first statement is executed.

  • The final state instance after the last statement is executed.

    • Some (non-terminating) computations don't have a last statement.

• A computation's history (or trace) is a sequence of state instances.

  • The history from start to end, or an interesting part of the total history.

  • Unchanged state instances are usually suppressed.

Predicate Logic

• A predicate is either

  • The constants T (true) or F (false), or

  • A relational operator ==, !=, <=, odd(), ... over state, or

  • The expressions P1 and P2, P1 or P2, P1 imp P2, or not P, where P, P₁, and P₂ are predicates, or

  • The expression forall i : P1 : P2, where P₁ and P₂ are predicates, or

  • The expression forsome i : P1 : P2, where P₁ and P₂ are predicates.

• The relational operators connect state with predicates.

  • Examples: i < 10, a[i] <= a[i + 1], divides(i, j).

  • Make these up as needed.

Predicate Operators

• The basic predicate operators are and, or, imp, and not.

  T and T = T		T or T = T
  T and F = F		T or F = T
  F and T = F		F or T = T
  F and F = F		F or F = F

  T imp T = T		not T = F
  T imp F = F		not F = T
  F imp T = T
  F imp F = T

• Implication (imp, also ->, also =>) is similar to if-then.

  • A true predicate can never imply a false predicate.

  • A false predicate can imply anything.

  • P1 imp P2' is equal to not P1 or P2.

  • Often used to specify choice.

Forall Predicates

• The predicate forall i : P1 : P2; is true when

  every value of i that makes P₁ true also makes P₂ true.

• P₁ and P₂ are usually functions if the index i.

• More than one index variable is allowed.

• forall is also known as universal quantification.

• Example:

  forall i, j : 0 <= i <= j < v.size() : v[i] <= v[j]
  

• What happens when P₁ is never true?

  • The forall is vacuously true.

  • Every i that satisfies P₁ also satisfies P₂.

• Note that

  forall i : P1 : P2
  

  is identical to

  forall i : true : P1 imp P2
  

Forsome Predicates

• The predicate forsome i : P1 : P2 is true when

  there is some value of i that makes both P₁ and P₂ true.

• P₁ and P₂ are usually functions if the index i.

• More than one index variable is allowed.

• Example:

  forsome i : 0 <= i < v.size() : v[i] == x
  

• forsome is also known as existential quantification.

• The particular index value are not of interest.

• The number of acceptable index values is not of interest.

  • As long as it's at least one.

State Predicates

• A state predicate is a predicate about a computation's state.

  • A non-trivial state predicate contains at least one relational operator.

• Given a state predicate and a state instance, the state instance satisfies the state predicate if the values in the instance result in the predicate evaluating to true.

  • Treat a predicate as a function over state instances: P(si).

  • P(si) is either true or false.

• A state predicate P defines a set of state instances { si such that P(si) is true }.

• A state predicate P₁ is weaker than a state predicate P₂ if the set associated with P₁ is larger than the set associated with P₂.

• A state predicate P₁ is stronger than a state predicate P₂ if the set associated with P₁ is smaller than the set associated with P₂.

• If P₁ is weaker than P₂, then P₂ is stronger than P₁.

A Programming Logic

• We can understand computations by understanding the its state transformations.

• We can characterize state with state predicates.

• We can understand computations with state predicates.

  • The state predicates indicate the desired state.

  • The computation performs the transformation to the desired state.

• The general scheme is { pre } S { post }, where

  • pre and post are state predicates.

  • s is a statement.

  • This is known as a Hoare triple.

• The triple { pre } S { post } holds if

  pre is true, and
  s executes to completion, and
  post is true.

Triple Fine Points

• Given the triple { pre } S { post }, what happens if pre is false?

  • The result of executing s is undefined.

  • s should only execute when pre is true.

• What happens if s never terminates?

  • The results of executing s is undefined.

  • This is known as partial correctness.

Procedure Pre- and Post-conditions

• Consider the procedure call { pre } P(...) { post }.

• pre is known as P()'s precondition.

  • The caller should make sure pre is true before calling.

  • P()'s behavior is undefined if pre is false.

• post is known as P()'s post-condition.

  • P() will ensure that post is true when it returns to the caller.

  • Assuming P() terminates (partial correctness.

• Example: linear search.

  • Purpose: return the index of a value in an array or -1 if the element is not in the array.

  • Precondition: true.

  • Postcondition: (i > -1 and a[i] = x) or <br> (i = -1 and forall j : 0 < j < |a| : a[j] != x)

Assignment Statements

• Consider { pre } x = e { post }.

  • We want post to be true after x = e executes.

  • What must be true before?

• x = e replaces the old value of x with e.

  • Replace every x in post with e;
    notationally, that's post[x <- e] .

  • The resulting predicate must be true before.

  • This is "going backward" through the assignment.

• If the predicate post[ x <- e ] is true
  then the triple { post[ x <- e ] } x = e { post }
  is valid by the Assignment Rule.

• Example: { ? } x = x + 1 { x = 3 }.

  • The postcondition is x = 3;
    the precondition is (x = 3)[x <- x + 1].

  • (x = 3)[x <- x + 1] simplifies to
    x + 1 = 3 simplifies to
    x = 2.

  • { x = 2 } x = x + 1 { x = 3 }

Statement Sequences

• Given { pre1 } S1 { post1 }
  and { pre2 } S2 { post2 }
  what should we do with S1 ; S2?

• The precondition to S1 ; S2 is clear.

  • It must be pre1.

• The postcondition to S1 ; S2 is clear.

  • It must be post2.

• What happens between S1 and S2?

  • post1 is true after S1 is done.

  • pre2 must be true before S2 starts.

  • Let post1 equal pre2.

• This will be loosened up in a few slides.

If Statements

• Next up: { pre } if B then S { post }.
  

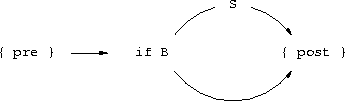
• pre and B is true true before S executes.

• post must be true after S executes.

• If S does not execute, then pre and not B must be true.

  • For post to be true, it must be that pre and not B imp post.

• If { pre and B } S { post } holds
  and pre and not B imp post is true
  then { pre } if B then S { post } holds too.

While Statements

• Next up: { pre } while B do S { post }.
  

• Suppose S never executes.

  • Then pre must equal post.

• When the while stops, then not B must be true.

• Before S executes, pre and B must be true.

• After S executes, pre must be true.

• If { pre and B } S { pre } holds
  then { pre } while B do S { pre and not B } holds too.

• There's no claim that the while ever ends.

  • This is partial correctness.

• The precondition is known as the loop invariant.

Weakening and Strengthening

• A stronger predicate is true less often than a weaker one.

  • x > 0 vs. x > 0 and odd(x).

• If P1 imp P2
  then P₁ is stronger than P₂.

• If P1 imp P2 is true
  and { P2 } S { post } holds
  then { P1 } S { post } holds too.

  • This is known as Strengthening the precondition.

• A weaker predicate is true more often than a stronger one.

  • mammal(p) vs. human(p).

• If P1 imp P2
  then P₂ is weaker than P₁.

• If P1 imp P2 is true
  and { pre } S { P1 } holds
  then { pre } S { P2 } holds too.

  • This is known as Weakening the post-condition.

Points to Remember

• There are many ways to understanding computations.

  • Debugging, mental execution, state descriptions.

• State descriptions are well suited for understanding computations.

  • Abstact and relatively simple

• Predicate logic can describe states.

  • Each predicate describes a set of valid states.

• A programming logic describes computations via predicates.

  • Using axiomatic semantics.

This page last modified on 7 August 2003.