- State-Based Notations
- State Machines
- States
- Transitions
- Events
- Statecharts
- Blobs
- Hyperedges
- Events
- Concurrency
- If I ask you to implement a program, you draw a flow chart.
- If I ask you to design an object-oriented system, you draw (many, many)
UML diagrams.
- What do you draw if I ask you to design and implement a concurrent
program?
- We'll be considering two notations: state machines, and Statecharts.
- These are both abstraction techniques.
- Representing too much detail in either is difficult.
- This is a general problem with state-based notations.
- A
state is some point in a computation's execution.
- Compare this to state instance covered previously.
- A state is usually labeled with a brief description.
- Other labelings are useful and important to consider.
- Example: the states of a computation using a critical section.
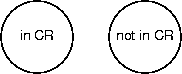
- There are many other states possible, depending on the level of
detail you're interested in.
- States and predicates can be usefully related.
- Label states with associated predicates.
- Given a state, derive the associated predicate.
- A (working) program doesn't stay in one state; it moves from state to
state.
- An arrow between two states represents a potential move between those
states.
- Each arrow is labeled with the reason for the move.
- Different transition labels lead to different kinds of finite state
machines.
- Transition labels range from code to predicates to brief text.
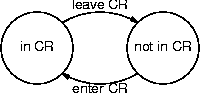
- Example: the transitions of a computation using a critical section.
- An
event is something that happens in the computation's
environment.
- An
input event starts in the environment and ends in the
computation.
- An
output event starts in the computation and ends in the
environment.
- An event can be represented by a state or a transition.
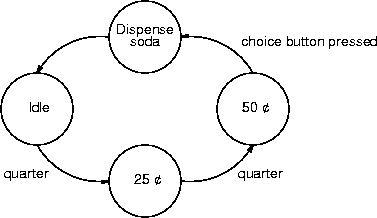
- Example: a soda machine.
- The combination of states, transitions, and events is called a
state machine.
- Only theoreticians worry about machines with an infinite number of
states.
- State machines are a well known system design and modeling technique.
- Hardware, embedded systems, and user-interfaces, for example.
- There are many tools supporting state machine creation, analysis, and
post processing.
- Different combinations of states, transitions, and events lead to
different kinds of state machines.
- Mealy machines have input events, Moore machines have output events.
- Mix 'n' match as needed, but understand what you're using.
- State machines are a simple but accurate representation for many
systems.
- Humans take to making and understanding state machines.
- There's lots of theory providing useful semantics for state machines.
- Graph theory to start with.
- State machines are a hospitable base for further extensions.
- Adding probabilistic transitions to get Markov systems.
- And don't forget the relation between state machines and regular
expressions.
- Useful semantics and easy understanding lead to techniques for
answering important questions.
- Reachability: does the system ever get to this state?
- Traces: by what steps can the system reach this state?
- What's wrong with this picture?

- There's only one thread; why bother with a critical section?
- Let's add another thread. What are the states now?
- There's two threads, each of which may or may not be in the CR.
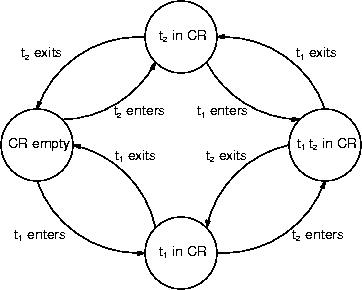
- Let's add another thread. Let's add n more threads.
- How many states are there now?
- Hint: use an n-bit number as node labels (don't peek).
- How can t1 and t2 be in the critical section?
- We forgot states for the entry and exit protocol.
- The two main problems with state machines are combinatorics and
hierarchy.
- It's easy to cause exponential state growth.
- Particularly when the system contains independent subsystems.
- Even sub-exponential growth can grow fast.
- Imagine adding an error state to a machine.
- State machines are flat, there's no where to hide extra states.
- A hierarchy of state machines provide abstraction.
- Sub-machines pop into and out of states at the next level.
- Neither of these problems bode well for modeling concurrent systems.
- A
blob is a simple, labeled curve enclosing space on the plane.
- Blobs may overlap arbitrarily.
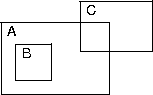
- Properly nested blobs indicate set containment.
- The elements of B are also elements of A.
- Not "blob B is an element of blob A."
- An
atomic blob is a properly nested blob that contains no other
blob.
- An atomic blob represents a state.
- B is an atomic blob, A and C are not.
- Blob overlap indicates the relation between blobs.
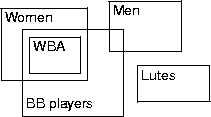
- Containment, disjointedness, common elements.
- How do you indicate the parts of A not in B, and vice versa?
- Actual blob elements must be represented by an atomic blob.
- Blobs Men and Women have no common elements.
- Blob WBA contains the common elements of blobs Women and Basketball.
- The atomic blob may not have any elements in it.
- Blobs are not like Venn diagrams in this sense.
- Depth of nesting indicates hierarchy.
- Zooming in and out reveals (in) or hides (out) parts of the hierarchy.

- Different blobs can be zoomed to different details.
- Zooming makes determining atomic blobs tricky.
- Really atomic blobs can't be zoomed into.
- Blobs are related by hyperedges.
- A
hyperedge is an arrow from a blob subset to a blob subset.
- From every blob in the subset to every blob in the subset.
- An edge is a special-case hyperedge
- Hyperedge heads and tails may cross blob boundaries.
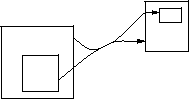
- Hyperedges are labeled with events.
- One event per hyperedge, although several per hyperedge are possible.
- An event e can be guarded by a predicate g.
- A transition on e[g] occurs only if e occurs and
g is true.
- If g is false, then e[g] does not occur, even if
e did.
- Guards include in(S), which is true if and only if state S
is active.

- A hyperedge ending at a non-atomic blob delivers the event to one of
the disjoint component blobs.
- At most one disjoint component blob can be active at any time.
- This is XOR decomposition.
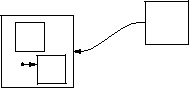
- A hyperedge starting at a non-atomic blob delivers the event from any
of the disjoint component blobs.
- The hyperedge has to have one head.
- A
statechart is a set of blobs, a set of hyperedges among the
blobs, and a set of events labeling the hyperedges.
- Harel defines statecharts as a specialization of higraphs.
- Statecharts were developed by David Harel in the late 1980s.
Statecharts: A Visual Formalism for Complex Systems, Science of Computer
Programming, Vol. 8, No. 3, 1987.
- Statecharts extend state machines in a number of ways.
- Orthogonality avoids combinatoric state explosions.
- State nesting provides a hierarchy of statecharts.
- There are other extensions, of which we will not speak, or speak of
only briefly.
- Statecharts are one of the many models included in the UML.
- The syntax and semantics differs between UML statecharts and Harel
statecharts.
- And whatever other statechart knock-offs are around, probably.
- The concurrent parts of a statechart appear in separate parts of the
same blob.
- The parts are separated by a dashed line.
- Each part contains a statechart disjoint from the all the other
statecharts.
- Each statechart in the blob is active.
- Unlike an XOR-decomposed blob, in which at most one statechart is
active.
- This
AND decomposition models concurrency.
- An event delivered to a concurrent blob is forwarded to each of the
constituent statecharts.
- This is like broadcast communication.
- Blobs and nesting provide modularity and hierarchy.
- Hyperedges are more compact than edges.
- Statechart decomposition grows linearly, not exponentially
- And decomposion is a concise and complete description of concurrent
behavior.
- On the other hand.
- Semantics can get tricky.
- Even with good semantics, analysis can get hairy.
- State machines are a useful way to represent small, nonconcurrent
systems.
- State machines do not scale well at all.
- Statecharts extend state machines with hierarchy and concurrency.
This page last modified on 14 August 2003.