CS 176, Introduction to Computer Science II

Summer 2001 - An Answer for Design Test 2

A simple-minded but useful fact serves as the basis for an algorithm for finding the largest square area of uniform value:

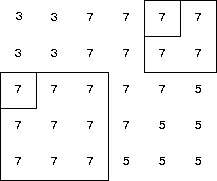
Every element in a m-by-n matrix is the upper-left element of a largest square area of uniform value.
The following picture shows two elements of a matrix and the associated largest square areas of uniform values having each element as the upper-left element:
example squares in a matrix
The algorithm follows immediately: consider each matrix element in turn, finding the largest square area of uniform value having the element as its upper-left element. If the square has a size larger than the current largest square, the algorithm has discovered a new largest square. This translates into the code 
// Input:
//   M - an m-by-n matrix of integers
//   m - the number of rows in M
//   n - the number of columns in M

largest_x = 0     // Of the upper-left element
largest_y = 0     // Of the upper-left element
largest_size = 0  // Size of the square

for 0 <= x < n
  for 0 <= y < m
    s = find_largest_square(M, m, n, x, y)
    if s > largest_size
      largest_x = x
      largest_y = y
      largest_size = s

return largest_x, largest_y, largest_size
where find_largest_square() returns the size of the largest square area of uniform value having its upper-left element at M[x,y].

Given this code, it's possible to answer question 2. Every matrix has a largest square area of uniform value, and one of the matrix elements must be the upper-left element of the square. This algorithm considers the largest square at each element in the matrix, and remembers the largest square found overall. This algorithm will eventually consider the element that's the upper-left element of the largest square and so the largest square will be discovered (but not necessarily remembered - it depends on whether or not the matrix has more than one largest square).

Unfortunately find_largest_square() isn't a standard C++ function, so before the other two questions can be dealt with, the details for find_largest_square() have to be worked out.

How should find_largest_square() find the largest square having its upper-left element at M[x, y]? Again, a simple fact helps find the answer:

There is always a largest square having an upper-left element at M[x, y]; at the least the square will have size 1.
This fact lets the previous question be rephrased as "Given that there exists a square area of uniform value of size s having its upper-left element at M[x, y], how can it be determined if there is a similar square of size s + 1?" A glance at a picture of the situation
growing the square
gives the answer: if the values in the dashed parts are the same as the values in the square, then s can be increased by 1 and we can ask the question again. Otherwise, the largest square has size s and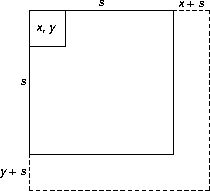 find_largest_square() is done.

When does this process stop? Either when a mismatch is found in the values or the square runs up against an edge of the matrix M.

With this explanation we can answer question 3. The algorithm starts with a single element and grows it by one row and column at a time until either a mismatch is found or there's no more matrix left. In either case the result is the largest square area of uniform value having the given matrix element as its upper-left element.

Putting the foregoing together gives the code 

find_largest_square(M, m, n, x, y)

  s = 1

  while x + s < n and y + s < m
    for 0 <= i < s
      if M[x + s - 1, y + i] != M[x + s, y + i]
        return s
      if M[x + i, y + s - 1] != M[x + i, y + s]
        return s
    if M[x + s - 1, y + s - 1] != M[x + s, y +s]
      return s
    s++

  return s
Because all this code is standard, the algorithm has now been completely described and the first question is taken care of.

This page last modified on 6 July 2001.