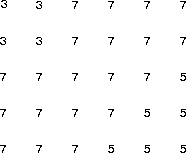
Given an m-by-n matrix of integers, m and n at least 1, it is always possible to find square areas of the matrix that have the same value (each element in the matrix forms a 1-by-1 square of uniform value). The size of a square area is the number of elements it encloses.
For example, the 5-by-6 matrix
has two 3-by-3 square areas of uniform value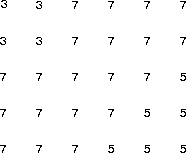
Each of these square areas has size 9. The matrix also has many 2-by-2 square areas of uniform value, two of which are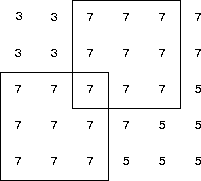
Develop an algorithm that accepts as input an m-by-n matrix of integers along with m and n and finds the largest square area of uniform value in the matrix (if there is more than one such square area, your algorithm can pick any of them).
Once you've developed the algorithm, do the following:
This page last modified on 1 August 2001.