One way to implement a dequeue with a circular buffer is to use two end indices, one indicating the front of the dequeue and the other the back of the dequeue. The empty-full problem occurs when the end indices have the same configuration when the dequeue is empty as when it is full.
One way to solve the empty-full problem is to prevent the dequeue from becoming full, which eliminates one of the two identical index configurations. Another solution is to keep count of the number of elements in the circular buffer.
See Nyhoff, page 223 for more information.
An in-place generic algorithm accepts a container reference and operates on the contents of the container, possibly changing the container. A copying generic algorithm accepts a two container references and copies the contents of one container to the other, operating on the contents while it's being copied.
See Musser and Saini, page 71 for more information.
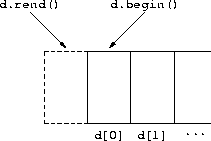
d be a non-empty dequeue. Do d.rend() and d.begin() refer
to the same value in d? Explain your answer.
No, they don't. d.begin() is an iterator referring to the first value in
d, while d.rend() is an iterator referring to the imaginary value
just past the end of the reversed d sequence.
It doesn't make much sense. Mutating generic algorithms change the contents of the containers passed in as arguments. If the container's original contents must be preserved, then combining the operation with a copy is more efficient than performing a copy followed by the operation.
Non-mutating algorithms, however, don't change the contents of their argument containers, so there's no particular reason to copy the containers before passing them to a non-mutating algorithm. Having copying versions of non-mutating algorithms would complicate things by increasing the number of generic algorithms without an offsetting advantage of increased execution-time efficiency.