Computer Networking Lecture Notes

14 February 2013 ♥ Data Communication

---

Outline

• Review and placement.
• Signals
• Representing signals.
  • Fourier series.
• Signals under transmission.
• Maximum data rates.
  • Nyquist’s and Shannon’s theorems.

Where Are We?

Get to here starting from here

Another View

• Networks look like this:

  

• However, networks also look like this:

  

  • Digital: a fake, two-valued world.
  • Analog: the real, infinitely-valued world.

The Physical Layer

• The physical layer mediates between a system and its environment.
  • A system: the host; an environment: the network.
• The physical layer does almost no networking.
  • It translates between digital and analog representations.
• The translation’s defined by physics, engineering, and the network.

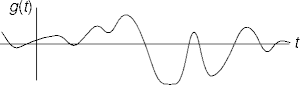
Signals

• A signal is a time-varying characteristic of a physical medium.
  • Voltage or current in a copper wire.
  • Displacement from rest in a piano string.
• A signal can be represented as a function of time g(t).

  

Periodic Signals

• A periodic signal repeats itself regularly.

  

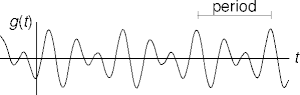
• The cycle is the smallest repetition unit.
• The period (wavelength) is the cycle length.
• A finite duration signal can be made periodic by repetition.

Example

• The ASCII representation for ‘b’ is 01100010.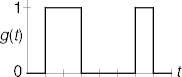

  

• Repeat g(t) to get the periodic signal g′(t).

  

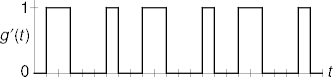
Frequency

• The frequency f of a periodic signal is the period p inverted.
  • p time per cycle.
  • f = 1/p Hz, Hertz or cycles per time.
• A parameter on variable t is a proportional knob for frequency.

  

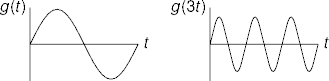
Representing Signals

Jean Baptiste Joseph Fourier 1768–1830

Fourier Series

• If g(t) is a periodic function with period T, then

  

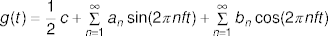
  where

  f = 1/T is the fundamental frequency.
  a_n, b_n are the nth harmonics.
  c is a constant.

  is the Fourier series for g(t).

Fourier Parameters

• Integrate g over the period T to find c:

  

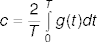
• Integrate to find the ith harmonics:

  

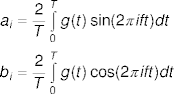
Parameters Example

• Given the periodic version of the ASCII ‘b’ function

  

• the Fourier parameters are

  

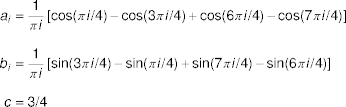
Approximation Example

Move the mouse over the upper coordinate of a harmonic plot to select that harmonic and all earlier ones.

Harmonics

• Each harmonic represents a component signal.
  • Higher harmonics represent higher-frequency signals.
• The first trade-off: harmonic count vs approximation accuracy.
  • The more harmonics included, the more accurate the approximation.
• But what’s the cost of including a harmonic?

Attenuation

• Attenuation is the lost of signal power due to “friction.”
• Most media attenuates higher frequencies more than lower frequencies.
• Unequal harmonic attenuation leads to signal distortion.
• One answer:
  • Don’t use harmonics that will be distorted.

Bandwidth

• Bandwidth is the frequency range assigned to a signal.
  • An FM channel has a 200 kHz bandwidth.
• A medium’s bandwidth is the frequency range over which attenuation is not too bad.

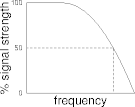
  “Not too bad”: ≤ 50% attenuation. There other definitions.

Maximum Data Rates

• A signal s has bandwidth B Hz.
• Nyquist’s sampling theorem:

  s can be exactly reconstructed from 2B samples per second.

• If s uses V discrete levels, then
  • maximum rate = 2B log₂ V bits/sec.
• For example: a 3kHz channel sending binary
  • 2·3,000 log₂ 2 = 6,000 bits/sec.

Signals and Noise

• Nyquist assumes a perfect errorless channel.
• Real channels have errors.
  • Modeled as random (thermal) noise (white noise).
• A channel has signal S and noise N.
• The signal-to-noise ratio (SNR, S/N) is
  • 10 log₁₀ S/N decibels (dBs)

Maximum Data Rates

• A noisy channel has bandwidth B and SNR E.
• The maximum data rate (capacity) is
  • B log₂ (1 + E) bit/sec.
• This is Shannon’s theorem.
• For example, a noisy channel has 1 MHz bandwidth and 40 dB SNR.
  • Capacity = 1 MHz log₂ (1 + 40) = 5.3 Mb/sec.

Summary

• A signal is a collection of harmonic signals (frequencies).
• Signal attenuation places constraints on signals.
  • In particular, finite bandwidth.
• Bandwidth and signals (levels or noise) lead to maximum data rates.
  • Either by Nyquist (levels) or Shannon (noise).

References

• Certain Factors Affecting Telegraph Speed by Henry Nyquist in the Bell System Technical Journal, July, 1924.
• A Mathematical Theory of Communication by Claude Shannon in the Bell System Technical Journal, July, 1948.

Credits

• Grenoble - ancien évêché - Joseph Fourier by Eusebius@Commons under a Creative Commons AT license.

---

This page last modified on 2013 February 14.