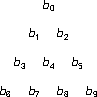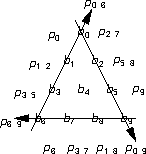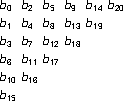Computer Networks, CS 414 & 514

Homework 2, 14 February 2013

This assignment is due no later than 1:00 p.m. on Monday, 25 February.

This homework assignment has five questions; answer all of them. Please site references you use to answer your questions, including the textbooks you’re using.

If you mail in your assignment, please send a printable document — a PostScript .ps or PDF .pdf document, for example — and not a source document — a Word .docx or Latex .tex document, for example.

1. Suppose bits are arranged in a triangular pattern:

   

   Assume there are enough bits to fill all sides. Three sets of parity bits can be computed, one set for each side in the triangle:

   

   What is the number of bit errors that can be detected and corrected by this triangular parity-bit arrangement? Justify your answer.

   ---

   A triangular arrangement of data bits is equivalent to a half-filled rectangular (square, because the triangle’s isosceles) bit array (Peterson and Daves, section 2.4.1):

   

   If exactly one row r (or column c) in the rectangle has any number of flipped bits, all errors can be reliably corrected by flipping the bits at the intersection of the columns (or rows) with parity errors and r (or c). Adding diagonals improves nothing in this case.
2. A laser beam with a 1 mm diameter is aligned to a detector with a 1 mm diameter so that the beam’s center coincides with the detector’s center. The laser gradually drifts out of alignment, and the detector loses contact with the laser when the beam center makes an angle of 0.5° with its correctly aligned position. What’s the distance between the detector and the laser? Assume the earth is flat; state other assumptions made. Show your work.

   ---

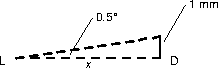
   Assuming the laser beam is not divergent, the beam’s center has to drift 1mm away from the detector’s center to lose contact with the detector:

   

   From any book on trigonometry ever written (Trigonometry, McKeague and Turner, chapter 1):

   1 mm/x mm = tan(0.5°)

   which gives

   x = 1 mm/tan(0.5°) = 114.6 mm

   about 4.5 inches.
3. Polynomials are easy to generate, but it seems that not all polynomials are equally suitable in CRC algorithms. Give an example showing what happens when the polynomial used in a CRC algorithm is chosen carelessly.

   ---

   At the sending side, a CRC generator polynomial G(x) transforms a message polynomial M(x) into a transmission polynomial T(x). At the receiving side, the received polynomial R(x) can be thought of as the sum of the transmission polynomial T(x) and an error polynomial E(x).

   By construction, G(x) divides T(x). If E(x) is non-zero (that is, errors occurred), G(x) should not divide E(x), otherwise errors will go undetected. If G(x) has only one term, it will divide any one-term E(x) with a term larger than G's (that is, one-bit errors can go undetected). A one-term generating polynomial would be a careless choice (unless you don’t care about single bit errors).

   If G(x) doesn’t have a three-term factor, then it’s possible G(x) may divide a two-term error polynomial, which would leave two bit errors undetected. A generating polynomial without a three-term factor would be a careless choice (unless you don’t care about two bit errors).
4. Consider the classic black-and-white paneled soccer ball

   

   Assuming panels that share a side, but not a vertex, cannot share a frequency, what is the smallest number of frequencies needed to make sure that it is possible to make a call in every cell on the soccer ball? Justify your answer.

   ---

   Assign a pentagon frequency A. The ring of five hexagons around the pentagon can be assigned the frequencies B, C, B, C, and D. Each pair of adjacent hexagons in the ring abut a second pentagon, which can be assigned the frequency A. The remaining hexagons around the second pentagon can be assigned frequencies in the same order as, and consistent with, the pattern used around the first pentagon. The remaining panels can be assigned frequencies in a similar way.

   It takes four frequencies to fully cover a soccer ball.

5. A channel achieves b bit/sec data stream using f MHz bandwidth and an n-level signal. The channel is reconfigured to use f′ MHz bandwidth and a n/2-level signal, but yet maintains a b bit/sec data stream. What is f′? Justify your answer.

   ---

   The number of signal levels have been halved, which removes one bit from the number of bits associated with each signal. The old bit rate was s sym/sec · n bits/sym; the new bit rate is s sym/sec · (n - 1) bits/sym. To make the new bit rate match the old,

   s sym/sec · n bits/sym = s′ sym/sec · (n - 1) bits/sym

   the symbols per second has to be adjusted:

   s sym/sec · n/(n - 1) = s′ sym/sec