Data Structures and Algorithms
CS 503

Quiz 3, 13 April 2011

1. True or false: A binary tree with ten nodes, exactly two of which are leaves, can be a balanced tree. Justify your answer.

   ---

   False. Because every path from the root ends at a unique leaf, each fork (two-child node) in the tree implies at least one different extra leaf in the tree. If a tree has exactly two leaves, it must have a single fork, which means the rest of the nodes have a single child (plus the two zero-child leaves). This means the tree must have a path traversing at least four consecutive single-child nodes, which is unbalanced at the first node (and probably elsewhere too).

2. How does the heap property ensure heap operations have O(log n) worst-case behavior?

   ---

   The second part of the heap property — that all leaves appear at levels i and i + 1 — makes sure that the differences in height between any node's subtrees is at most one.

3. A valid binary search tree T contains the 100 numbers 1 through 100. Does the number sequence 64, 32, 42, 17, 33 represent a path from the root to the node containing 33 through T? Justify your answer.

   ---

   T’s root value is 64, which means its left subtree contains the values 1 through 63 and its right subtree contains the values 65 throught 100. The second step in the path is 32, which is contained in T’s left subtree. Note this means all remaining values in the path are constrained to in the range 1 through 63.

   T’s left subtree has root value 32, which means its left subtree contains the values 1 through 31 and its right subtree contains the values 33 through 63. The next step in the path is 42, which is greater than 32, and the path moves to the right subtree.

   The next step in the path is 17, which is impossible because the right subtree contains the values 33 through 63. The path 64, 32, 42, 17, 33 cannot represent a path through T.

4. You are given five coins; four are real and one is counterfeit. The only way to distinguish between the real and counterfeit coins is by weight: the counterfeit coin is lighter than a real coin. What is the minimum number of weighings needed to determine the counterfeit coin? Justify your answer.

   ---

   Let the coins be numbered 1 through 5, i:j mean “compare the weights of coin i and j”, and a node with just i mean i is the counterfeit coin. One set of weighings that discovers the counterfeit is

   

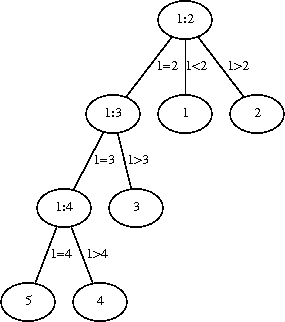
   Because there is only one counterfeit coin, if 1 = 2 then both are real coins. This tree is not balanced; can it be balanced?

   The reasoning that coins 1 and 2 were real if 1 = 2 can be applied to pairs of coins: if 1 + 2 = 4 + 5, then they all must be real. This leads to the minimal balanced tree

   

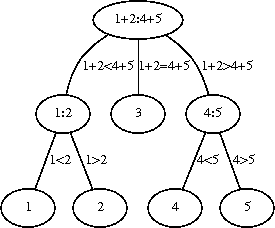
   This tree is minimal because removing any more weighing nodes removes the possibility of reaching the correct answer.

5. ---