The free list threads through the next-index array to keep track of the unused array elements, which makes finding an unused array element fast (independent of the array size).
Without a free list, finding a free array element requires searching the next-index array for an unused array element, which takes time proportional to the array size.
what is the smallest number of check-marks needed to describe a data structure that can act as either a stack or a queue? Justify your answer.
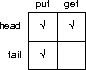
Three check marks are needed to describe a data structure that can act as either as a queue or a stack (or both). To be a stack, elements should be added to and removed from the head; to be a queue, elements should be added to the tail and removed from the head:
It's not possible to implement a deque having fast operations using queues because elements can be added and removed at either end of a deque, and a queue only supports one operation at each end.
It is possible to implement a deque using several queues, but supporting put and get at both ends requires shifting values between queues, which takes time proportional to the number of elements in the deque and so is not fast.
size() method
without using an instance variable keeping track of the number of elements.
Clearly state your assumptions.
The easiest solution is to assume the tail index points to the next free array location to receive a new element, if such a free location exists (otherwise the array is full and the size is n, the array size). With that assumption, the size would be the head minus the tail pointer, except the head may wrap around and be behind (be less than) the tail pointer. The easiest way to deal with the head lagging the tail is to add n to the head to make sure it's never less than the tail. However, the resulting difference has to be reduced modulo n to (possibly) adjust the difference back into range.
Alternatively, the head and tail indices could be kept as always increasing values, which never let the head lag the tail and allow a simple subtraction to find the size (it also makes the difference between full and empty buffers obvious). However, the head and tail indices would have to be reduced modulo n when used to access an array element, which is an expensive operation to perform on each array access.
Your colleague inserted the new value as a successor to the given value, and then swapped the two values to restore the proper order, which invalidated references to the old value.
Adding a successor is always fast because it follows the next pointers; adding a predecessor is not fast because it goes against the next pointers, requiring a trace down from the head. A doubly linked list has a fast insert-before operation, but it doesn't invalidate any references when used, unlike your colleague's solution.