Data Structures and Algorithms Lecture Notes

2 March 2011 • Performance Estimation in Practice

Outline

Array Searching.
Vector storage management.

What Does This Algorithm Do?

int find(int a[], int x)

  for (int i = 0; i < |a|; i++)
    if a[i] == x
      return i

  return -1

Look for a value in an array.

What Does This Algorithm Do?

int find(int a[], int x)
  l = 0
  r = |a|
  while l < r
    m = (l + r)/2
    if a[m] == x
      return m
    if a[m] <= x
      l = m + 1
    else
      r = m
  return -1

Which algorithm is better?

Assumptions

When looking for something, faster is better.
Statements take time to execute.
- Different statements execute in different times.
- Ignore that and just count the number of statemets executed.
Input: The array size in elements.
Output: a worst-case estimate of the number of statements executed.

Let's Estimate!

int find(int a[], int x)

  for (int i = 0; i < |a|; i++)
    if a[i] == x
      return i

  return -1

What are we counting?
- Comparisons, or maybe statements (same thing).
What's the driver?
- The size of the array.

Basic Statements

Count the number of comparisons (or statements, or expressions) executed.
Assume array.length == n.

  for (int i = 0; i < |a|; i++) : O(1)
    if a[i] == x : O(1)
      return i : O(1)

  return -1 : O(1)

Choice Statements

  for (O(1); O(1); O(1)))
    if O(1) : O(1)
      O(1)

  O(1)

The if statement executes O(1) + O(1) = O(1) comparisons.

Iteration Statements

  for (O(1); O(1); O(1))) : O(1)
    O(1)

  O(1)

The for loop iterates O(n) times.
- O(1) comparisons per iteration * O(n) lines.

Statement Sequences

O(n)

O(1)

O(n) + O(1) = max(O(n), O(1)) = O(n).
The number of comparisons performed worst case is proportional to the number of lines read.

Second Program

Reduce the basic statements.

  l = 0 : O(1)
  r = |a| : O(1)
  while l < r : O(1)
    m = (l + r)/2 : O(1)
    if a[m] == x : O(1)
      return m : O(1)
    if a[m] ≤ x : O(1)
      l = m + 1 : O(1)
    else
      r = m : O(1)
  return -1 : O(1)

Conditional Statements

O(1)
O(1)
while O(1)
  O(1)
  if O(1)
    O(1)
  if O(1)
    O(1)
  else
    O(1)
O(1)

O(1)
O(1)
while O(1)
  O(1)
  if O(1) : O(1)
    O(1)
  if O(1)
    O(1)
  else
    O(1)
O(1)

O(1)
O(1)
while O(1)
  O(1)
  O(1)
  if O(1) : O(1)
    O(1)
  else
    O(1)
O(1)

Compound Statements

O(1)
O(1)
while O(1)
  O(1) : O(1)
  O(1)
  O(1)
O(1)

O(1) + O(1) + O(1) = O(max(1, 1, 1)) = O(1)

Looping

How often does the while loop iterate?

  while l < r
    m = (l + r)/2
    if a[m] ≤ x
      l = m + 1
    else
      r = m

O(1)
O(1)
while O(1) : O(log n)
  O(1)
O(1)

O(log n)*O(1) = O(1*log n) = O(log n)

Finishing Up

O(1)
O(1)
O(log n)
O(1)

Sequential statements:
O(1) + O(1) + O(log n) + O(1) =
O(max(1, 1, log n, 1)) =
O(log n)
O(n) vs. O(log n): the second program wins!

Static Arrays vs. Dynamic Data

Once allocated at compile time, static-array size can't be changed.
- Static arrays don't work well with dynamic amounts of data.
- Run-time size information usually isn't available at compile time.
The result is usually too much wasted space or too little storage space.

Dynamic Arrays

Run-time storage management resolves static storage vs. dynamic data.
- Allocate arrays at run-time.
  - Size arrays exactly with run-time information.
  - Replace a too-small array with a larger one.

Implementation

class sequence
  Object data []
  int next-data

  append(T e)

    if next-data ≥ data.length()
      Object new-data [] = 
        new Object [data.length() + 1]
      for i = 0 to data.length() - 1
        new-data[i] = data[i]
      data = new-data

    data[next-data++] = e

Appending Costs

How much does an append cost?
- It depends. Does the sequence have extra space or not?
What's the worst-case cost for append?
- Worst case, every append resizes storage.
```
sequence<Integer> is
for i = 0 to 100
  is.append(i)
```

Worst-Case Analysis

if next-data ≥ data.length() : O(1)
  Object new-data [] = new 
    Object [data.length() + 1] : O(1)?/O(n)
  for i = 0 to data.length() - 1 : O(1)
    new-data[i] = data[i] : O(1)
  data = new-data : O(1)
data[next-data++] = e : O(1)

if O(1)
  O(1) or O(n)
  for O(1) : O(n)
    O(1)
  O(1) or O(n)
O(1)

Worst-Case Appending

if O(1)
  O(1) or O(n)
  O(n)
  O(1) or O(n)
O(1)

if O(1)
  O(n)
O(1)

O(n)
O(1)

O(n)

In the worst case, appending does work proportional to the size of the sequence.

So?

Is doing work proportional to n so bad?

Consider

sequence<Integer> is
for i = 0 to 100
  is.append(i)

How much work is going on here, worst case?

Sloppy Analysis

for i = 0 to n : O(1)
  is.append(i) : O(n)

In each iteration append() does O(n) work in the worst case.
```
for O(1) : O(n)
  O(n)
```
Loading the sequence takes O(n²) work.

Less Sloppy Analysis

for i = 0 to n
  is.append(i)

In each iteration append() does work proportional to i.
The total amount of work performed by append() is proportional to
1 + 2 + ... + n = n(n + 1)/2 = O(n²)
Loading a sequence can take O(n²) work.

Better Behavior

Can append() have better behavior? How?
- “Better” means “asymptotically less.”
How about amortizing the amount of work done on each append?
- Reallocate and copy every t appends, rather than on every append.

Amortized Sequences

class sequence
  Object data []
  int next-data
  unsigned a = 50

  append(T e)

    if next-data ≥ data.length()
      Object new-data [] = 
        new Object [data.length() + a]
      for i = 0 to data.length() - 1
        new-data[i] = data[i]
      data = new-data

    data[next-data++] = e

Worst-Case Analysis

The code changes in only one place.

 if next-data ≥ data.length() : O(1)
  Object new-data [] = new 
    Object [data.length() + a] : O(n)
  for i = 0 to data.length() - 1 : O(1)
    new-data[i] = data[i] : O(1)
  data = new-data : O(1)
data[next-data++] = e : O(1)

And the change isn't enough to effect the code's asymptotic behavior.

Amortization Effects

In this case, amortization isn't powerful enough to reduce asymptotic complexity.
Does amortization have any effect at all?
Consider
```
for i = 0 to n
  is.append(i)
```
with amortizing sequences.
With sloppy analysis, append() still does O(n) work on each iteration, worst case.

Less Sloppy Analysis.

Define “work” to mean “copy elements from old to new.”
```
for i = 0 to n
  is.append(i)
```
In each iteration append() does no work, or work proportional to i.
- When i = ja, append() does work proportional to ja.
  - a the amortization amount; j a positive integer.

Less Sloppy Analysis..

In total, append() does work proportional to
0 + ... + a + ... + 2a + ... + ja = n
a(1 + 2 + ... + j) = aO(j) = O(j) = O(n)
Loading a sequence still take O(n²) work.
- But amortization has reduced the constant.

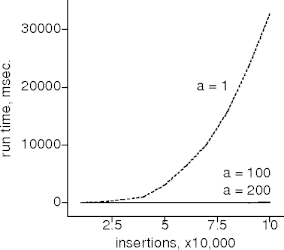
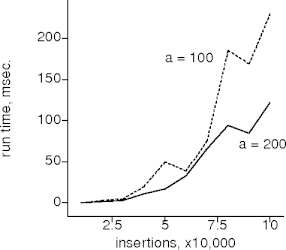
Does It?

amortization in effect

See the code; see the data.

Asymptotically Better Behavior

Can append() have asymptotically better behavior? How?
Adding a constant factor isn't powerful enough, in some sense.
Multiplication is a more powerful form of addition.
Will multiplying by a constant factor have enough oomph to change the asymptotic behavior?

Multiplicative Sequences

class sequence

  Object data []
  int next-data

  append(T e)

    if next-data ≥ data.length()
      Object new-data [] = 
        new Object [data.length()*2]
      for i = 0 to data.length() - 1
        new-data[i] = data[i]
      data = new-data

    data[next-data++] = e

Analysis.

What happens to
```
for i = 0 to 100
  is.append(i)
```
The sloppy analysis remains unchanged.
- Worst case, append() does O(n) work in each iteration.
The less-sloppy analysis is almost unchanged.
- When i = 2^j, append() does work proportional to 2^j, j a positive integer.

Analysis..

In total, append() does work proportional to
0 + 2⁰ + 2¹ + 0 + 2² + ... + 2^j, 2^j = n

2⁰ + 2¹ + ... + 2^j = 2^{j + 1} - 1

= 2*2^j - 1

= 2n - 1

= O(n).
Doubling the storage size asymptotically reduces the amount of work.

Does It?

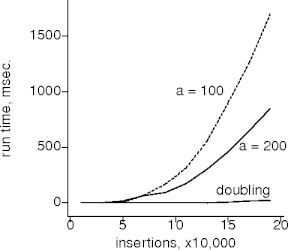
amortization vs doubling

Summary

For better performance, find an asymptotically better algorithm.

This page last modified on 2010 March 2.

2⁰ + 2¹ + ... + 2^j	= 2^{j + 1} - 1
	= 2*2^j - 1
	= 2n - 1
	= O(n).