Data Structures & Algorithms
CS 305 & 503

Quiz 3, 13 April 2010

1. A colleague of yours has implemented a binary tree (not a binary search tree) in which each node holds the depth of the subtree for which it is the root. Explain how the depth can be exploited by the operations searching, inserting, and deleting nodes from the tree. Do not describe how the depth should be maintained for these operations, just explain how it can be exploited by these operations.

   ---

   Generally, knowing the subtree heights in a binary tree isn’t too useful because the data are unordered, and most non-constant worst-case operations are going to be linear in the number of nodes in the tree.

   Inserting: inserting a new node into a binary tree is a constant-effort operation (create a new root with the old root, if any, as a child). Exploiting subtree height while inserting data could create balanced trees, but insertion becomes more expensive (logarithmic effort) and the other operations can’t take advantage of the balance.

   Searching: searching for a node in a binary tree takes linear worst-case effort, and knowing the subtree heights provides no advantage during the search. There might be some average-case advantage to searching the subtree with smaller height first, but without further information about the binary-tree structure it is unclear the advantage would offset the smaller probability of successfully searching the smaller subtree.

   Deleting: deleting a node from a binary tree takes worst-case effort linear in the number of nodes in the tree to find the node, and again linear worst-case effort to remove the node if found. There may be some small advantage to finding a replacement node in the child subtree with the smaller height, but in the absence of a scheme to maintain overall balance it is unclear what the advantage may be.

   The answers, in no particular order and approximately verbatim:

   1. Searching, inserting and deleting nodes can be used to exploit the depth because the depth is the value in the node.¹ When searching, inserting, and/or deleting a node, knowing the depth of nodes makes it easier to do any of these operations.²

      1: One of the values, anyway.

      2: How?

   2. Each depth will be exploited by the operations because of the fact that they will constantly be changed each time one³ is implemented.⁴ Inserting adds nodes to the tree, causing an imbalance in parent-child relations, as well as deleting nodes. The more unbalanced these depths are the harder it is to traverse through the tree.⁵

      3: One what? Operation?

      4: What’s being implemented? Operations?

      5: Why does an unbalanced tree make it harder to traverse the tree? It may take longer in an unbalanced tree to get to one leaf than another leaf, but how is it any harder?

   3. One important part of a tree is its balance. By exploiting the depth data it is possible to maintain a somewhat balanced tree. For insertion, the tree is supposed to add nodes at the bottom (leaves) of the tree.⁶ If a root knows the depth of its subtrees than it can insert on the side that has a lower depth,⁷ stopping the tree from going further out of balance. The same goes for deletion. When a node needs to be deleted it is supposed to be replaced by a leaf node. By knowing the depth the tree can follow the deepest path and switch that with the node to be deleted. While searching depth can also be exploited because if the node knows the depth of the subtrees, it can know it is at the top of the tree or at the bottom or somewhere inbetween.⁸

      6: True, but the new value can also be inserted as a new root.

      7: Or perhaps less depth, indicating leaves closer to the root.

      8: How is that an advantage in searching? And is the advantage greater than searching the subtree with less depth first?

   4. The depth can be exploited by the search operation in order to sort the tree⁹ and subsequently make searching considerably easier. Because the depth of the subtree is known, the search could potentially first look at the subtree with less depth, thus finishing the quicker of the two subtrees first (one could potentially be empty, for example). The depth can also be exploited by the insert operation in that the knowledge of the depth could assist in balancing out the tree after the insert operation occurs. Knowing the depth would answer the question of knowing which nodes to rotate and how they would affect the balance of the tree.¹⁰ The depth’s part in the delete operation is essentially the same. Keeping track of the depths after deletion could maintain the balance of the tree and be an indicator of when a subtree is becoming too excessive or minute.

      9: Sort how? By depth or by value stored?

      10: True, but maintaining balance wasn’t part of the question.

   5. In any tree the simplest place to insert values is on the ends¹¹ as leaf nodes.¹² For insertion, we know that the largest number¹³ in any node has to be the end of the tree (the lowest depth), allowing us to insert onto the end.¹⁴ We can also use this knowledge for searching and deletion.¹⁵ To delete, we must search for the value first. Since we know the depths we can find the values within that specific depth without having to traverse the entire tree.¹⁶ To delete, after we find the value we need, simply drag it down to the lowest depth (the greatest node) and delete it.¹⁷

      11: The ends of what?

      12: Because you’re not dealing with binary search trees, wouldn’t be easier to insert a new value at the root; that requires no traversal at all.

      13: What number? The depth?

      14: How does insertion work in a binary tree without depth information?

      15: The depth isn’t necessary to find a leaf. It is necessary to find the deepest leaf (furthest away from the root), but that’s forcing the insert to do the maximum amount of work.

      16: How does that work? What’s the relation between values stored in the tree and the depths at which they’re stored?

      17: But that also takes the maximum amount of work. Why not take the leaf at least depth?

   6. The depth could be exploited by these operations because you can see how far through the tree you must go while searching.¹⁸ Therefore exploiting the depth.

      When inserting a node, the node will then hold the depth of which subtree it is at.¹⁹

      Also, when deleting a node you will exploit the depth because if it²⁰ is not a leaf, then a node will be bubbled up into its place. Therefore exploiting the depth.²¹

      18: Searching goes far enough into the tree to find what it’s looking for, then it stops. What does that have to do with depth?

      19: True, but is that an advantage? If it is, how is it exploited by insert()?

      20: Presumably the node being deleted.

      21: How does that exploit depth? It reads like the same algorithm used to delete a node in a tree without depth information.

   7. Through searching, the values²² would not change and would not be exploited.²³

      With insertion and deletion, the values must be changed and if they are not changed after every move, the data inside each node would be wrong.²⁴ If you did not do this all values above the new or deleted node, including the root would be off.

      22: The depth or the key?

      23: What about looking in the shallower subtree first?

      24: True, but is there any way to exploit the depths when inserting and deleting?

   8. For searching, the depth can be used to choose which subtree to search first. By choosing the subtree with less depth first, the method can increase its efficiency.²⁵

      For inserting, the depth would not help since the new value would be added at the top to become the new root.

      For deleting, the depth can be used to choose which subtree to traverse to find the leaf fastest. Once the quickest path to a leaf is found, than its value can be hoisted up to the node to be deleted.

      25: On average; in the worst case searching’s still O(n).

2. The histogram

   

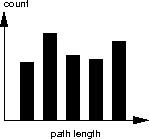
   shows the path lengths in a binary tree. Is the binary tree balanced? Justify your answer.

   ---

   The easiest way to answer this question is to draw a small balanced binary tree and count the paths. It should quickly lead to the conclusion that a balanced tree has 2ⁱ nodes with path length i, which means the histogram should look exponential:

   

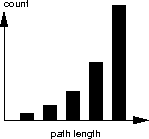
   The given histogram isn’t exponential, so the associated binary tree can’t be balanced, or can’t be well balanced.

   Alternatively, you could observe that if a tree is balanced, then all leaves can be found at level i or i + 1 for some i. The three path lengths starting at the second from the left have decreasing count, which means there are leaves at each of those path lengths (or corresponding levels). Because leaves appear at more than two consecutive levels, the tree can’t be balanced.

   The answers, in no particular order and approximately verbatim:

   1. A tree is balanced when its subtrees do not differ in levels¹ by more than 1. In this case the binary tree seems to be unbalanced because the path lengths differ by more than 1.²

      1: In height.

      2: What’s the relation between path length and subtree height?

   2. No, I believe this binary tree is unbalanced. It would have been balanced if each path length’s count was the same.³ Therefore each path would have been gone through the same number of times.⁴

      3: Is such a thing possible in a binary tree?

      4: What? What does it mean to go through a path? Traverse it?

   3. It is possible that this binary tree is balanced. Since we do not know the numbers for the count it is possible that the count is split evenly among the subtrees.⁵ If that is the case than this tree could be balanced when balance is defined as any two subtrees differing in height by at most 1. Since there is a height count at the largest path length it is probable that the subtree⁶ from the root each have a path at this path length.⁷

      5: The absolute numbers aren’t important; it’s the relation between them that matters.

      6: Which subtree? There may be two of them.

      7: More than probable; it is certainty, otherwise the path length wouldn’t have been counted.

   4. No, it is not balanced because the root and parent nodes should have much shorter path lengths then the children.⁸

      8: The children’s path lengths will be one more than the parent’s path length, which isn’t much shorter. More distant descendants will have shorter path lengths. And how do you tell the parents from the children from the histogram?

   5. It depends on the definition of “balanced.”⁹ In a case where balance is defined by the leaf nodes being unequal by no greater than one node,¹⁰ then no, the tree would be imbalanced. Reason being that the histogram bars are too different in length.¹¹

      9: This is a bad way to start an answer.

      10: What does it mean for leaf nodes being unequal?

      11: The bars are not different enough.

   6. The binary tree is balanced because the path lengths are not that far apart from one another so their distances¹² are not greater than one.

      12: Maybe “differences”?

   7. To be balanced, the path lengths of a node’s children must not differ by more than 1.¹³ In a histogram, you would expect to see the count rise fairly evenly as the path length increases, showing a tree where each level has roughly equal nodes.¹⁴ This histogram shows uneven count fluctuations as path length increases, showing a tree that differs significantly per level as path length increases. This binary tree is not balanced.

      13: Assuming a node has children, it’s not possible for the children’s path lengths to be different: each child has a path length one more than the parent’s path length.

      14: What are roughly equal nodes?

   8. The binary tree isn’t balanced. This is because, judging by the number of paths, one of the binary subtrees is null.¹⁵ This cannot happen, as a tree must consists of either two subtrees.¹⁶

      15: Which subtree? There are a lot of them.

      16: True, but one (or both) of the subtrees could be empty.

3. The kthSmallest() method for a binary search tree ADT accepts the integer k and returns the kth smallest value in the bst. For example, bst.kthSmallest(0) returns the smallest value in bst, and bst.kthSmallest(bst.size() - 1) returns the largest value. What traversal would provide the simplest and most efficient implementation of kthSmallest()? Justify your answer. Do not be concerned with illegal values of k.

   ---

   Starting at the root, assume the left subtree contains l nodes. If k ≤ l, then the left subtree contains the kth smallest value and the algorithm should traverse to the left subtree and start over. If k = l + 1, then the root contains the kth value and the algorithm’s done. Otherwise k > l and the right subtree contains the kth smallest value; the algorithm should recurse down the right subtree, looking for the (k - (l + 1))th smallest value. This algorithm implements an in-order traversal.

   The answers, in no particular order and approximately verbatim:

   1. Post-order traversal would provide the simplest and most efficient implementation of kthSmallest() due to the fact that once you traverse the left child you have an idea of all the smallest values¹ then you traverse the right and find/order those values. Once you have the orders of both the left and right you have the full order except for the root which will be the middle term.² This traversal will give you a fast access to the ordering of the children and then automatically place the root as the middle.

      1: But what particular idea do I need to know about the smallest values to find the kth smallest value?

      2: But the root comes after both the left and right children in a post-order traversal, so how does it get to the middle?

   2. The traversal that would provide the simplest and most efficient implementation of kthSmallest() would be to first traverse the root node, then the left or right nodes depending on the value stored in k.³ The reason for starting at the root is that presumably k is either less than or grater than the value held by the root.⁴ If it is less, the ADT can traverse the left nodes in an efficient time. If it is greater, the ADT can instead traverse the right nodes. If k equals the value found at the root, the traversal is finished and the number of the traversals will be, in the best possible case, only 1.

      3: Depending how? Also, what kind of traversal behaves like this?

      4: k has no direct relation to the values stored in the tree; it is an ordinal position.

   3. Preorder traversal would be most efficient because it checks the root first and then the left and right children.⁵ This is good because you only have to compare parents and children and not cousins.

      5: But before you check the root, don’t you have to know how many children are in the root’s left subtree? If the left subtree contains more than k children, then there’s no need to check the root.

   4. • In order traversing goes from the left node to the root, and then to the right node.⁶
      • Pre ordering (usually the faster way because you start at the root)⁷ goes from the root to the left then right subtree.
      • Post order traversing goes from the left tree to the right subtree, then the root.

      I would say, to implement the kthSmallest() method the most efficient is traversing through using a post order traverse. This is because the smallest value in a BST is found at the left most node, the largest is at the right most node of the tree.⁸ You can get to the smallest first in post order and if you want the largest value, that would be the next node to check in post order traversing.

      6: From the left subtree, to the root, then to the right subtree.

      7: All traversals start at the root, but they process the root at different times during the traversal.

      8: Right, but kthSmallest() isn’t interest in the largest or smallest value, just the first or last value.

   5. Since in a binary search tree everything to the left of the root is smaller than the root and everything to the right is greater than or equal to the root,⁹ the most efficient implementation of kthSmallest() would be to go down the left most subtree and work up to the root.¹⁰ Then go down the right subtree also on the leftmost side since everything to the left is smaller than the right. So for example: where the # inside the node represents the data value stored and it would represent k in the kth smallest value. It is checking the nodes in the form of LNR. Starting from the left, then checking the node, and moving to the right.

      9: What does the relative sizes of the node values have to do with anything?

      10: Why work up to the root? What kind of work is needed?

   6. Since maintaining the BST property¹¹ requires everything for the least of the root to be less than the value stored there, and everything to the right has to be at least that value, we already know where to search.¹² The smallest value will be the left most node, and the largest value will be the right most node. Performing a binary search in the tree would be most efficient. Since a binary search will compare values it finds to avoid traversing too far down a path it doesn’t need to go. This, giving us fairly simple and efficient traversal through our tree.

      11: The kthSmallest() method doesn’t change the tree; why is maintaining the BST property important?

      12: By what information? k is an ordinal number, not a value stored in the tree.

   7. Pre-order traversal (NLR) would provide the simplest and most efficient implementation of kthSmallest(). We talked in class that this was the fastest traversal¹³ and since k could be any value within the tree, it would be best to start at the root and work our way down.¹⁴ This way it would only be long if “k” was the very least or most value in the tree.

      13: For searching, but this is a different operation.

      14: What useful can be done at the root before knowing how many values each child has?

   8. The inorder traversal would provide the simplest and most efficient implementation due to its LNR path. The method is looking for the smallest value in reference to k. In a BST, the smallest values are always on the left, then the node, than the right.¹⁵ This method isn’t searching for a specific value, it is looking for a location and then returning the value at that location. Since it is asking for the smallest value, it should start on the left and go in order to the right.

      15: The smallest values, relative to the root, are only on the left; the larger (or no smaller) values are on the right.

4. merge() is a common operation to include in a heap ADT. h1.merge(h2) adds the values in h2 to h1. Assuming heaps are implemented using arrays, provide a worst-case asymptotic analysis of the heap merge algorithm. You should assume the heap parameter (h2 in the example call) is left unchanged by the merge.

   ---

   merge() can be implemented as

   void merge(heap h)
     for i = 0 to h.size() - 1
       add(h.elements[i])
   

   Adding and element to a heap takes O(log n) worst case. N elements are added to the heap, for a total of O(n log n) work, where n can be the sum of the sizes of h1 and h2.

   The answers, in no particular order and approximately verbatim:

   1. In the worst case scenario the array would be full that you are adding h2 to. Therefore, in a dynamic array implementation, a new larger array would have to be created. In this would generate O(n²) because all the values from h1 must be copied from the old array and inserted into the new array, as well as adding the values from h2.¹

      1: But is it resonable to assume that every insertion into h1 will resize the array?

   2. The worst case asymptotic analysis would be O(n). This is because although you are adding h2 to h1 you will still go through the array and touch each element one time, just as you would with h1. h1 was already O(n)² already so O(n) + O(n) = O(n).

      2: What is it that is O(n) in h1?

   3. The worst case asymptotic analysis of the heap merge algorithm is when merging into a already full array; this causes overflow. So adding the values of h2 to h1 can possibly cause more work.³

      3: More work than what? And how much more work?

   4. merge() would add the entire h2 heap to a rear of h1. Any leaf will do, therefore only half of the h1 heap would be traversed to find a leaf.⁴ The entire h2 heap would then be bubbled-up to maintain the heap property. Since half of the original heap can be ignored for this merge, the worst-case asymptotic analysis would be O(log n).⁵

      4: Why would you need to traverse the heap at all? The next available leaf is at the end of the occupied array elements.

      5: Per new leaf, or for all leaves?

   5. The worst case asymptotic analysis is that one has to rearrange the heap to maintain the heap property with every value of the new heap, which means that you traverse through the heap n amount of times.⁶

      6: True, but how much work gets done on each traversal through the heap?

   6. The heap merge operation is basically adding every value of h2 to h1. Since we are doing a worst case analysis I am going to assume the array for h1 becomes full and we are going to have to make a new array and adding all the values from the old array as well as the new values from the array being added. This causes merge() to have linear behavior or O(n).⁷

      7: How much work gets done as each value is added to the heap?

   7. The merge would have to look at each value of each heap to add them correctly while maintaining the heap property, which would be linear O(n) behavior.⁸

      8: Per value added, or in total?

   8. The problem with merge() is that once h2 is added to h1, the order of the heap will require resorting. This will require rotating and searching the heap in order to reobtain balance. From a worst case standpoint, the most iterations done by the algorithm to balance out the effects of the merge would be O(n), where n = h1 + h2.⁹

      9: And how much work is done per iteration?

This page last modified on 15 April 2010.