Outline
- Storage management.
- Delayed storage recovery.
- Free lists.
- Another array-based linked-list ADT.
A Dynamic-Array Pathology
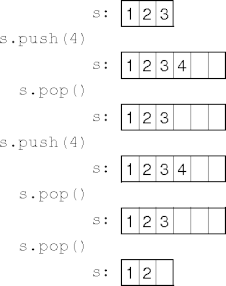
- Frequently crossing the same resize point causes highly inefficient
execution.
- Queues suffer from this problem too.
Adding Delay
- Rather than reacting immediately to a resize point, delay until sure.
- Delay is asymetric: expansion can't be delayed.
- Define a low-water mark below the resize point.
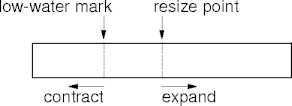
- Delay contraction while the ADT size is above the low-water mark.
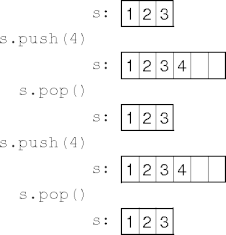
Delay Example
Controlling Delay
- Delay can be specfied as a percentage (p% below the resize point)
or absolutely (a elements below the resize point).
- The client can set the delay, or the ADT can, or they both can.
- Clients know more about their application, but get things wrong and
may not recognize the problem.
- The ADT is always aware of the problem, but may not know the best way
to solve it.
Dynamic Linked Sequences
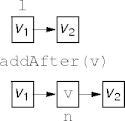
void addAfter(T v)
Link l = findBefore(v)
Link n = new Link()
n.value = v
n.next = l.next
l.next = n
|
|
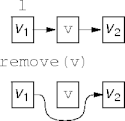
void remove(T v)
Link l = findBefore(v)
l.next = l.next.next
|
|
Boxed code creates nodes and garbage (unreferenced instances).
Dynamic Storage Costs
- Creating new nodes and collecting garbage is expensive.
- Although dynamic-storage managers have gotten good at their job.
- Large linked lists with much turnover may have unacceptable performance
due to storage management.
- What can be done to reduce storage-management costs?
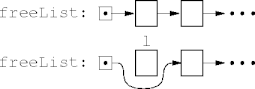
Free Lists
- The usual solution to garbage problems is recycling.
- Move unlinked nodes to a free list; they're not garbage any more.
- Check the free list before allocating new nodes.
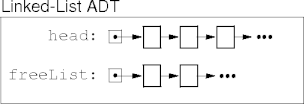
Link management
private Link newLink()
if freeList != null
Link l = freeList
freeList = l.next
return l
return new Link()
|
|
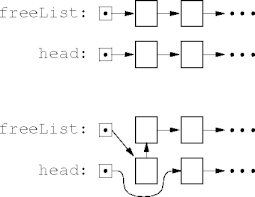
public void remove(T v)
Link n = findAfter(v)
Link l = n.next
n.next = l.next
l.next = freeList
freeList = l
|
|
Oh Really?
- Generate 100,000 pairs of adds followed by removes.
- Add runs are (rand(10) + 1)*10 long.
- Remove runs are rand(ll.size()) + 1 long.
- Java 1.6.17 on an elderly single-core laptop.
- No compiler or JVM command-line options.
- Free-list manged code runs 1.8 to 2 times faster than new +
garbage-collected code.
- Ten-run average: 1.9, 0.02 std dev.
See the the code; see an example run.
Free-List Problems
- If linked-list size is bimodal (large and small), the free list may
have too many unused links.
- This is a similar to large mostly empty arrays, and handled in the
same way.
- Use a low-water mark to avoid free-list thrashing.
- If free-list links continue to reference values, they may obstruct
value garbage collection.
- Null out the value field(s) when hanging a link on the free list.
Linked-List Comparison
| | List | List |
|---|
| | (Array) | (Node) |
|---|
| create | | fast | fast |
|---|
| delete | | fast | fast |
|---|
| add | | slow | fast |
|---|
| remove | | slow | fast |
|---|
| traversal | | fast | fast |
|---|
| navigation | | slow | slow |
|---|
| dynamic | | no | yes |
|---|
- fast: single-element operation.
slow: potentially n-element operation.
Dynamic-Array Lists
- Using a dynamic array gives dynamic linked lists.
- But dynamic arrays won't do anything about slow add and removes.
- Values in the array still have to be moved around.
- How can dynamic arrays be used to provide fast adding and removing?
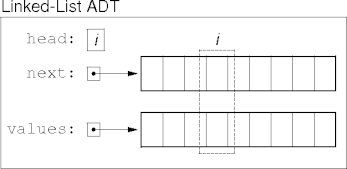
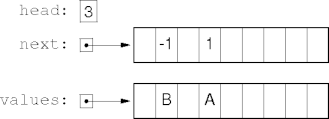
Faster Array Linked Lists
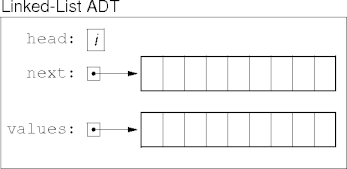
-
values[i] is the value stored in link i.
-
next[i] is the index to link i’s successor.
Link Definition
Example
- A dynamic linked list:
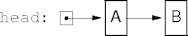
- The equivalent linked array implementation:
Linked-List Comparison
| List | List | List |
|---|
| (Array) | (LArray) | (Node) |
|---|
| create | fast | fast | fast |
|---|
| delete | fast | fast | fast |
|---|
| add | slow | fast | fast |
|---|
| remove | slow | fast | fast |
|---|
| traversal | fast | fast | fast |
|---|
| navigation | fast | slow | slow |
|---|
| dynamic | no | no | yes |
|---|
- fast: single-element operation.
slow: potentially n-element operation.
Summary
- Expensive operations should not be performed frequently.
- Make them less expensive or less frequent if they are.
- Spread an operation's cost over as many payers as possible.
- Explicit adjacency relations allow fast value manipulations, even in
arrays.
|
This page last modified on 16 February 2010.
|

|