Data Structures & Algorithms Lecture Notes

23 February 2010 • Asymptotic Estimates

Outline

Algorithms and Programs
Asymptotic Estimates
A Behavior Hierarchy
Structural Analysis

A Program

Program 1.

int find(int a[], int x)

  for (int i = 0; i < |a|; i++)
    if a[i] == x
      return i

  return -1

Another Program

Program 2.

int find(int a[], int x)
  l = 0
  r = |a|
  while l < r
    m = (l + r)/2
    if a[m] == x
      return m
    if a[m] <= x
      l = m + 1
    else
      r = m
  return -1

Which program is better?

Program Analysis

There are many programs, all different.
Which program can be judged suitable?
- It depends on your criteria.
- Memory use, speed, message count, ...
Start with execution time.
- Performance is usually related to other criteria.
  - It takes time to use a resource.
Program performance can be measured or estimated.

Determining Performance

Measure execution time.
It’s a definitive measure.
But algorithms don’t execute; they’re not code.
- It requires implementing the algorithm.
There are other problems too.

Problems

Measurements are context dependent.
- Determining context accurately is difficult.
Comparing results is hard.
- Contexts must match to be meaningful.
Meaningful measurements are hard.

Estimated Performance Analysis

If you don’t know, guess (or estimate).
- Ignore the details, go for the big picture.
- Estimating is simpler than measuring.
Skillful professionals estimate well.
- Estimation is a skill to develop.

Estimation Advantages

Estimates are more comparable then are measurements.
- The context is mostly ignored when estimating.
Estimates are more durable than are measurements.
- Not as closely tied to hardware or software technology.

Modeling Algorithms

Model the algorithm by counting important parts of the algorithm.
The algorithm is reduced to a count, other details abstracted away.
Make sure you understand what's being counted.

Sorting Example

Model a sorting algorithm by counting
- the time it takes to sort n elements.
  - Or the number of comparisons done.
  - Or the number of elements moved.

Database Example

Model a distributed-database algorithm by counting
- f(n) is the number of messages it takes to perform a transaction.
- Or the time it takes to commit a transaction.
- Or the number of times a transaction is overtaken and aborted.

Asymptotic Estimates

Counting can be tedious and difficult to get right.
Rather than count, estimate the count.
- There are many ways to estimate counts.
An upper bound on f(n)'s behavior is useful.
- It represents potential worst-case behavior.
- Other bounds are possible, but harder to find.

Upper-Bound Estimates

An upper bound of f(n)’s behavior is a function g(n) with the property that
C*g(n) >= f(n)
as n grows without bound for some positive constant C.
- That is, f(n) is never larger than g(n).
- It’s an asymptotic estimate because n grows without bound.

Big-Oh Notation

An alternative representation for f(n)'s upper bound is O(f)
- That is, g(n) = O(f).
This is only part of the story.

Asymptotic Estimate Properties

For any f(n), f(n) = O(f).

Estimate Addition

O(f) + O(g) is O(max(f, g)).
- Larger estimates swallow up smaller estimates.
- max(f, g) may not exist as n grows without bound.

Estimate Multiplication

O(f)*O(g) = O(fg).
- The product of estimates is the estimate of the product.

Estimate Quality

Suppose g = O(f) and h = O(f).
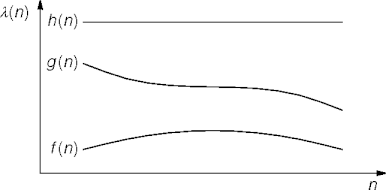
- If h = O(g), then g is a tighter estimate of f than is h.

A Behavior Hierarchy

A function hierarchy.

Constant O(1) hash table searching

Log O(log n) binary search

Linear O(n) linear search

Log-linear 0(n log n) heapsort

Quadratic O(n²) bubble sort

Cubic O(n³) matrix multiplication

Exponential O(2ⁿ) optimal route finding

Polynomial order - quadratic, cubic, and so on.

Constant Behavior

constant behavior

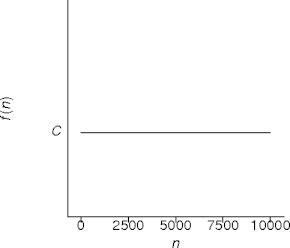
This is input-independent behavior
- This is the ideal behavior.
- But watch out for the value of C.

Logarithmic Behavior

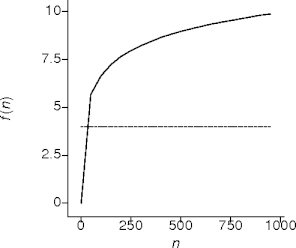
log behavior

This is repeated dividing behavior.
- Binary search.

Linear Behavior

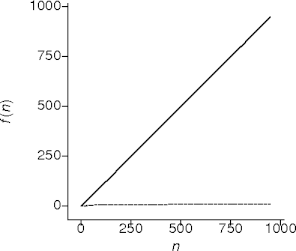
linear behavior

This is touch every element behavior.

Log-Linear Behavior

log-linear behavior

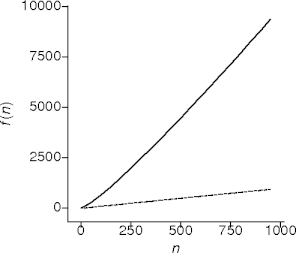
This is sorting behavior.
Repeatedly divide for every element.

Quadratic Behavior

quadratic behavior

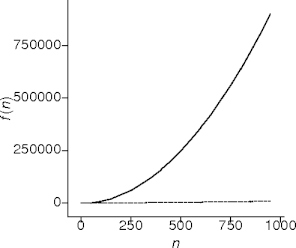
This is double loop behavior.

Cubic Behavior

cubic behavior

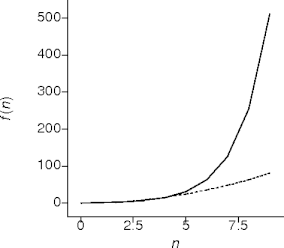
This is triple loop behavior.
- Matrix multiplication.

Exponential Behavior

Exponential behavior

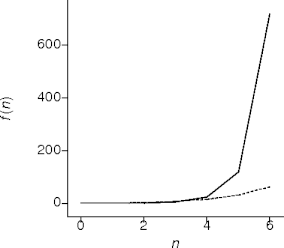
This is systematic guessing behavior.

A Family Portrait

Let n = 100.

f f(n)

C C

log n 4.6

n 100

n log n 460.5

n² 10,000

n³ 1,000,000

2ⁿ 1,267,650,600,228,229,401,496,703,205,376
Except for small n, improving asymptotic behavior is important.

f	f(n)
C		C
log n		4.6
n		100
n log n		460.5
n²		10,000
n³		1,000,000
2ⁿ		1,267,650,600,228,229,401,496,703,205,376

Structural Analysis

Algorithms have a regular structure.
- Statements, sequences, loops, and choice.
Use program structure to derive asymptotic estimates.
- Assign behavior to smaller units.
- Combine units following algorithm structure to find behavior of larger units.
- Repeat until the whole algorithm’s been combined into a single estimate.

Running Example

Swap sort.

i = 0
while i < n
  j = i + 1
  while j < n
    if a[i] > a[j]
      std::swap(a[i], a[j])
    j++
  i++

Let n be the array size in elements.
Let f(n) be the number of elements moved.

Statements

Usually O(1), but know your data structures.
- Compare vec.size() with lst.size().

Estimate the simple statements.

i = 0 while i < n j = i + 1 while j < n if a[i] > a[j] std::swap(a[i], a[j]) j++ i++

O(1) while i < n O(1) while j < n if a[i] > a[j] O(1) O(1) O(1)

`if` statement

if b s₁ else s₂
Execute either s₁ or s₂, but which one?
- Because we’re overestimating, use the larger of the estimates.
Don’t forget b's cost.
- O(f_b) + O(max(f₁, f₂))

`if` Example

Estimate the if statements.

O(1) while i < n O(1) while j < n if a[i] > a[j] O(1) O(1) O(1)

O(1) while i < n O(1) while j < n O(1) + O(1) = O(1) O(1) O(1)

Statement Sequence

s₁ ; s₂
s₁ is O(f), s₂ is O(g), so s₁; s₂ is O(f) + O(g)
What is O(f) + O(g)?
- Treat O(f) as a set of functions, pick a representative function and apply the definition of big-oh.
- Take the larger of the two.
  - O(f) + O(g) is O(max(f, g))

Sequence Example

Estimate the statement sequences.

O(1) while i < n O(1) while j < n O(1) O(1) O(1)

O(1) while i < n O(1) while j < n O(1) + O(1) = O(max(1, 1)) = O(1) O(1)

Loops

while b do s
s has asymptotic estimate O(f).
s gets executed some number of times.
- Asymptotically bound the number of times as O(g).
The estimate is O(f)*O(g).
- O(f)*O(g) is equivalent to O(f*g)

Loop Overhead

The loop itself does constant work per iteration.
- Work associated with iteration operations and guard testing.
You can
- ignore it, or
- include it in the estimate.
An implicit, and occasionally troublesome, assumption.

Loop Example

Estimate the loop.

O(1) while i < n O(1) while j < n O(1) O(1)

O(1) while i < n O(1) O(n)*(O(1) + O(1)) = O(n) O(1)

To Finish

Estimate the statement sequence.

O(1) while i < n O(1) O(n) O(1)

O(1) while i < n O(1) + O(n) + O(1) = O(n)

Loop Estimate

O(1) while i < n O(n)

O(1) O(n)*O(n) = O(n²)

Sequence Estimate

O(1) O(n²)

O(1) + O(n²) = O(n²)

Done: O(n²).
In the worst case, swap sort moves O(n²) elements when sorting an n-element array.
The structure of the algorithm determines the next step.

Subroutines

Non-recursive subroutines are treated like a statement.
- Guess at or know the estimate for a call.
Recursive calls are tougher.
- Solved with recurrence relations.
- Later for that.

Subroutine Example

What is the estimate on each of these loops?

while vec.size() > 0
  vec.erase(vec.end() - 1)

while vec.size() > 0
  vec.erase(vec.begin())

Things to Watch

Keep an eye on the constants.
- Asymptotically identical algorithms may be (usually are) different.
- For small n, constants are more important - linear search is usually good enough.
Estimate the right things.
- What’s important: an expensive algorithm, or the number of times it’s called?

Further Considerations

Look at the right inputs.
- Focus on what’s driving the algorithm.
- Worrying about execution time on communication-bound computations.

Summary

Develop algorithms not programs.
- Code programs from algorithms.
Use performance criteria to select algorithms.
Use asymptotic estimates for performance.
Estimate performance using structural analysis.
- Let the algorithm give you the next step.
Understand what the estimates are saying.


Constant	O(1)	hash table searching
Log	O(log n)	binary search
Linear	O(n)	linear search
Log-linear	0(n log n)	heapsort
Quadratic	O(n²)	bubble sort
Cubic	O(n³)	matrix multiplication
Exponential	O(2ⁿ)	optimal route finding