Chaining would be better. Because collisions are expected, an open-addressed scatter table will form clusters, and separate clusters may merge into one-another, defeating the purpose of using location-sensitive hashing.
The trick is to find the largest element to replace; it could be among any of the leaves in the heap. Searching the whole heap takes O(n) work; searching the leaves only also takes O(n) work, but with a smaller constant. Another possibility, mentioned in the text, is to maintain a max-heap at the other end of the array; the largest element will be at the root of the upside-down heap.
The important observation to make is that if edge e is a bridge, then it must be incident to at least one articulation point because removing that node removes e, and so disconnects the graph, which is what an articulation point does.
However, the other node incident to e need not be an articulation point if it is only incident to the bridge (if it is incident to other edges, then it too is an artiulation point).
The second observation also brings up a special case: both nodes incident to the bridge might have no other incident edges. In this case neither point is an articulation point but the edge is still a bridge.
if |G.E| = 1 and |G.V| = 2
return G.E
else
A = the set of articulation point in G.
B = the set of bridges for G, initially empty.
for articulation point p in A
for e in the set of edges incident on p
if both ends of e are in A
add e to B
else if the end of e not in A has no other incident edges
add e to B
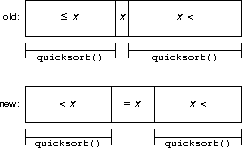
Partitioning could be changed: instead of gathering one pivot value in the array, all of them could be gathered in a block. Once gathered, recursion occurs at the ends of the block.
Each recursive iteration of quicksort effectively removes one value from the sort. Because there are only a small constant number of values, this turns quicksort from a O(n log n) sort to a O(n) sort with a constant C, the number of different values appearing in the sort.