CS 503 Quiz 4

CS 503, Advanced Programming I

Quiz 4, 20 March 2007

  1. A binary-tree node may contain, in addition to pointers to its children, a pointer to its parent. Explain how parent pointers can be exploited when a) searching, b) inserting, and c) deleting nodes from the tree. Do not describe how the parent pointers should be maintained for these operations, just explain how they can be exploited by these operations.

    In all cases a parent pointer eliminates the need for a stack to traverse the tree. However, parent traversals require at least one extra bit per node to keep track of revisits, which is an O(n) amount of extra space for a tree with n nodes vs odrlgn() extra space for a stack (assuming a balanced tree; O(n) stack space otherwise).

  2. A binary tree T is both a binary search tree and a heap. Analyze the worst-case performance of a search through T.

    All the values in the left child of the root of a binary-search are less than (let us say) the value at the root and all the values in the root's right child are at least the root's value. All the values of both children of the root of a heap are at least (let us say) the root's value. If T is both a heap and a binary search tree, it must be the T has no left child because otherwise the heap property would be violated.

    A heap is balanced; that is, the absolute difference between the heights of the children of a node is at most 1. Because T is a heap and has no left child, it either has no right child or its right child is a leaf.

    Because T has one or two nodes, the worst-case search time is constant.

  3. A heap is a balanced binary tree. A binary tree of n nodes can be balanced in many ways. Is there a particular way of balancing a binary tree that's best when using the tree as an array-implemented heap? Explain.

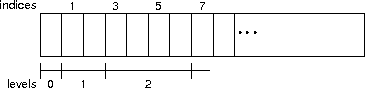
    Heap node i's children are at 2i + 1 and 2(i + 1); that is, they are adjacent to one another in the array. Heap node i's sibling's children are laid out adjacent to node i's children via their common parent at 2(i - 1) (because node i has a sibling, it can't be the root and must have a parent). Children of nodes at a particular level are laid out adjacent to one another on the next level, filled in from to left to right. Not only does this balance the heap, it left balances it because there are not gaps in the occupied array elements.

    heap layout in an array

  4. A colleague of yours asks you to point to one of three identical wallets on a table, telling you that two of the wallets are empty and the third contains a 10-dollar bill, which you may keep if you pick the wallet containing it. After you chose your colleague picks one of the remaining wallets and shows you that it's empty. Your colleague then asks you if you'd like to change your mind and pick the remaining wallet or stick with your original choice. Draw a tree (not necessarily binary) to help determine what you should do.

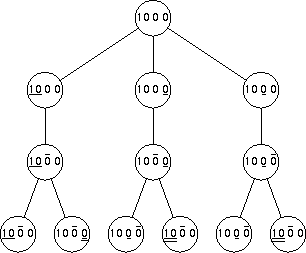
    Label each node in the tree with the amount of money in each wallet ($10 or 0). Your initial pick is indicated by an under bar; your colleague's response is indicated by an over bar; a double under bar indicates your changed choice.

    the monty hall problem

    If you don't change, you have a one in three chance of picking the right wallet; if you do change you have a two in three chance. Your odds are better if you change your mind (remember, the more you know, the smarter your choice).

This page last modified on 10 April 2006.