CS 503 Quiz 3

CS 503, Advanced Programming I

Quiz 3, 27 February 2007

The cyclic assignment
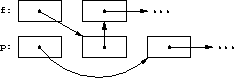
```
cyclic_assign(a, b, c)
  t = a
  a = b
  b = c
  c = t 
```
assigns b's value to a, c's value to b, and a's value to c; that is, it rotates the values cyclically one to the left. Show how cyclic assignments can be used to delete the element following p and hang the deleted element on the free list f in the following situation:

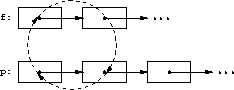
Starting with the situation picture above, we want to end with
using a cyclic assign. The picture tells us everything we need to know:
- p should be pointing to what p.next is currently pointing to.
- p.next should be pointing to what f is currently pointing to.
- f should be pointing to what p is currently pointing to.
or
which is
```
cyclic_assign(p.next, p.next.next, f.next)
```
Suppose you have to sort a singly-linked list without auxiliary data structures (that is, no copying data into a separate array). Which of the ~~searches~~ sorts we have covered in this course would be best for the job? Justify your answer. The quality of your answer is directly proportional to the number of ~~searches~~ sorts it considers.
As was mentioned in class, quicksort with an auxiliary array works best (at least for the examples shown). However, because auxiliary data structures aren't allowed, heapsort seems the best choice for two reasons. First, it has worst-case O(n log n) behavior, and second the splitting and merging can be done efficiently without artifice on singly-linked lists.
Without specific context information, it's a toss-up for the O(n²) sorts. Selection sort seems bad because it requires splicing individual links in and out of the list, which is a complication. However, it's also possible to move just the data in the links rather than the links themselves, eliminating the need for complicated link manipulations. The same observation applies to all the O(n²) sorts, which leads to the generic recommendations that bubble sort is least plausible and insertion sort might be the best with selection sort somewhere in the middle.
Explain why using block allocation in a linked list could cost O(n) extra time.
Once a block of n link elements has been allocated, they need to be hung on the free list; that requires n linking operations for O(n) work.
A colleague of your argues that a dequeue can be made as efficient as a singly-linked list. Do you agree with your colleague? Explain.
Unless there's some wizzy trick up your colleague's sleeve, you should probably disagree. The sticking point with dequeues is deleting from either end of the list. In a singly-linked list, deleting from the down-stream end requires going up-stream, which requires an O(n) traversal of the list from the other end. Three of the dequeue operations take constant work on a singly-linked list, but the fourth takes O(n) work.

This page last modified on 3 March 2006.