• Up to the minimal available capacity of adjacent pipes.

Ford-Fulkerson Method

• Developed in 1962 by Lester Ford and Delbert Fulkerson.

• An iterative method starting from zero flow.

  • Find a general flow path and increase capacities along the path.

  • Repeat until no more improvements can occur.

    • Every general flow path has no available capacity (positive or negative).

Correctness

• Delete an at-capacity edge from every general flow path in the network.

  This is a network cut. When the flow across a cut equals the outflow, the outflow is maximal.

• This is (part of) the min-cut max-flow theorem.

Convergence

• Floyd-Fulkerson does not discriminate among available flow paths.

  • Sometimes this is a problem.

Flow-Path Choice

• Choose the shortest non-full general flow path from inlet to outlet.

  • Use breadth-first search.

  • Bounds the iterations to O(VE) for O(V³E) behavior.

• Even better: chose the maximal-capacity general flow path.

  • Use a modified Dijkstra's algorithm.

  • The priority is available capacity.

Performance

• The max-flow choice variation

  • takes O((V + E) log V) per iteration, and

  • requires O(1 + log_M/(M-1) f) iterations.

    • M is the number of edges in a cut.

    • f is flow cost.

Network-Graph Representations

• Either representation works.

• The tricky bits are:

  • Storing the actual- and maximum-capacity weights.

  • The graph is "undirected directed".

  • The undirected graph has asymmetric positive and negative weights (flows).

Variations

• Maximal network flows is an important and heavily studied problem.

• Variations include:

  • Multi-commodity flows (hard).

  • Vertex constraints and undirected edges.

  • Minimum-capacity edges (hard).

  • Considering edge costs too (hard).

Hospital Residencies

• A medical student must complete a residency at a hospital.

• Each year, in order of decreasing preference,

  • each medical student lists hospitals and

  • each hospital lists medical students.

• The problem is to match students and hospitals stably and maximally.

Graph Matching

• Given a graph G, a matching for G is a subgraph of G such that

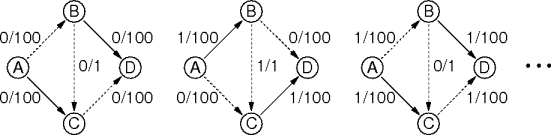
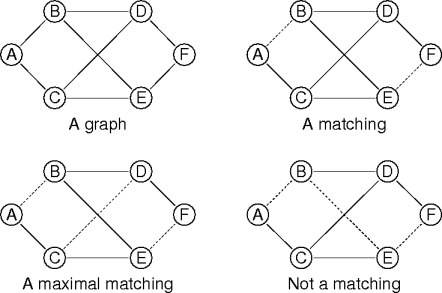
  E_M ⊆ E_G and 2|E_M| = |V_M|

  That is, every vertex in M is adjacent to exactly one other vertex.

• A maximal matching for G has the largest number of edges among all possible matchings for G.

  • Ideally V_M = V_G, but not always.

Example Matchings

Problem Structure

• The residency-assignment problem has more structure than just a graph.

  • There are two types of vertices: students and hospitals.

  • Students pick only hospitals and vice versa.

    • Students don't pick students; hospitals don't pick hospitals.

• Understand your data, the better to exploit it.

Bipartite Graphs

• A bipartite graph is a graph with the additional properties

  • V can be partitioned into V₁ and V₂.

  • E ⊆ V₁×V₂.

  Bipartite edges run only between the two subsets.

Bipartite Matching

• Now the problem is to find a maximal matching for a bipartite graph.

A Maximal-Flow Solution

• Transform the bipartite graph into a network:

  Add a inlet and outlet. Make each edge directed with a maximum capacity of one. Now find the maximal flow.

• At-capacity edges are part of the matching.

Example Solution

Max-Flow Properties

• It's a matching: each bipartite vertex can appear in at most one edge.

  • All edge capacities are at most 1; one unit in, one unit out.

• It's maximal: any more matching edges imply a larger than maximal flow.

• It's more efficient: each flow path adds an edge to the matching.

  • There are at most |V|/2 iterations.

Preferences

• A good solution to the student-hospital matching problem should cater to preferences.

  • Students prefer hospitals, hospitals prefer students.

• Each vertex rank-orders vertices in the other set.

  A: 2 5 1 3 4 B: 1 2 3 4 5 C: 2 3 5 4 1 D: 1 3 2 4 5 E: 5 3 2 1 4

  1: E A D B C 2: D E B A C 3: A D B C E 4: C B D A E 5: D B C E A

Stable Matchings

• Each vertex should be matched with its most preferred partner.

  • Disappointments are inevitable.

• An unstable match can be improved by swapping partners.

  A: 7 1 2 B: 4 2 1

  1: F A B 2: E B A

  A: 7 1 2 B: 4 2 1

  1: F A B 2: E B A

• Find a stable matching (or marriage).

A Simple Approach

Iterative Matching

• Each hospital goes down its list, trying to match its most preferred student.

• Each student accepts or rejects each hospital request.

• A student may break an already agreed upon pairing to get a better one.

• An accepted then rejected hospital continues down its list.

Example Iterative Matching

A: 2 5 1 3 4 B: 1 2 3 4 5 C: 2 3 5 4 1 D: 1 3 2 4 5 E: 5 3 2 1 4

1: E A D B C 2: D E B A C 3: A D B C E 4: C B D A E 5: D B C E A

Data Structures.

• Each hospital needs to know its list of students and its currently paired student.

  • A matrix preferences with a row per hospital.

  • A vector student with an element per hospital.

• preferences[h,student[h]] is hospital h's current pairing.

  • preferences[h,++student[h]] is the next one.

Data Structures..

• Each student needs to know its current pairing and whether or not a requesting hospital is better than its paired hospital.

  • A matrix rank with a row per student indexed by hospital.

  • A vector hospital with an element per student.

• Should student s accept hospital h?

  • rank[s,h] > rank[s,hospital[s]]

Stable Matching Algorithm

• Assume there's n hospitals.

  for h' = 1 to n
    h = h'
    do
      student[h]++
      s = preferences[h, student[h]]
      if rank[s, h] > rank[s, hospital[s]]
        swap(hospital[s], h)
    while h > 0
  

Algorithm Properties

• It terminates: each do-while iteration increases some hospital's preference.

• It's stable: every student s's more preferred hospitals are paired with students they prefer more than s.

Variations

• There are many stable matchings; some favor the requesters over the grantors.

  • The requesters are more satisfied than are the grantors.

• The requester order is irrelevant.

  • The first requester to ask has no advantage over the last requester to ask.

  • A consequence of allowing grantors to revoke earlier agreements.

The Grand Tour

• A grand tour is the shortest route though a set of cities.

  • Each city is visited once.

• The grand-tour problem (traveling salesman problem) accepts a set of cities and finds a grand tour.

Graph Representation

• The set of cities can be represented as a weighted (assume connected) graph.

  • Two vertices (cities) are adjacent if there's a direct road between them.

  • The edge weights are the road miles between adjacent cities.

• A grand tour is related to a Hamiltonian path (or circuit).

First Cut

• How about a path-coherent depth-first search?

  bool 
  grand_tour(graph g, vertex v, int l)
    if l == g.vertices().size()
      return true
    v.visited = true
    for n in g.neighbors(v)
      if not n.visited
        if grand_tour(g, n, l + 1)
          return true
    v.visited = false
    return false
  

Performance

• grand_tour(), in the worst case, explores every possible path.

  • There are O(!V) possible paths.

• Unfortunately, this is the best that can be done.

  • The Hamiltonian-path or -circuit problem is intractable.

  • The Grand-Tour problem is also intractable.

Approximate Solutions

• Intractable problems are size-limited.

  • Somewhere between 35 and 500 cities.

• Another approach is to trade-off tractability for optimality.

  • Producing an almost-optimal solution may take much less time.

Points to Remember

• Graphs model many important problems.

  • Planing or optimizing traveling, flowing, or matching.

• Graph models look the same.

  • Maybe you've already solved this problem.

• It doesn't take too much for a graph problem to become complicated.

References

• Network Flows, Chapter 33, Matching, Chapter 34, and Exhaustive Search, Chapter 39 in Algorithms by Robert Sedgwick, Addison-Wesley, 1983.

• Maximum Bipartite Matching, Section 27.3 in Introduction to Algorithms by Thomas Cormen, Charles Leiserson and Ronald Rivest, MIT Press, 1990.