Outline
- Asymptotically faster sorting.
- A fast O(n2) sort.
- A worst-case O(n log n) sort.
- A worst-case O(n) sort.
Faster Sorting
|
|
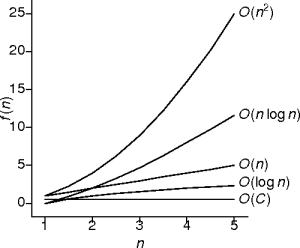
- The previous sorts were all O(n2).
- Can we do better?
- How much better can we do?
|
- Remember:
It's faster only when it's asymptotically faster.
A Question Reasked

- The question can't be answered until the array's completely sorted.
- Not quite:

- This answer doesn't require sorting.
Partitioning
partition(T a[], int left, int right)
T pivot = a[left]
int l = left + 1
while l < right
if (a[l] ≤ pivot) l++
else if (pivot < a[right - 1]) right--
else swap(a[l++], a[--right])
swap(a[left], a[--l])
return l
Quicksort
- Partitioning divides the array into thirds.
- Repeatedly call partition on the unsorted parts
quicksort(T a[], int left, int right)
if right > 1 + left
int mid = partition(a, left, right)
quicksort(a, left, mid)
quicksort(a, mid + 1, right)
Quicksort Analysis
-
partition() does O(n) work.
- N elements divide in "half" O(log n) times.
- Each half gets passed to
quicksort(), and so to partition().
- Remember, constants (2 here) don't matter.
- O(log n) iterations, O(n) work per iteration.
- Quicksort sorts with O(n log n) work.
Oh Really?
Well, No
-
partition() may not divide into halves.
- The pivot may be an extreme value.
- This has two consequences:
-
partition() does little useful work.
- There are O(n) instead of O(log n) iterations.
Is It?
- Worst-case behavior occurs on mostly sorted data.
Avoiding Worst-Case Behavior
- Avoid worst-case quicksort behavior by
- Not using quicksort on sorted data.
- Randomly permuting the data.
- Making a more artful pivot-value choice.
Artful Pivot Choices
Do They Work?
- Worst-case behavior is still O(n2).
- But it has a low probability of occurrence.
Rigorous Halving
- Quicksort slows down when it can't divide the data evenly.
- Consistent, even halving results in O(n log n) behavior.
- Is there a sort organized around consistent, even halving?
Divide to Conquer
- Now recurse on the two halves.
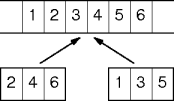
Reuniting Divisions
- A segment of size less than two is sorted.
- Two sorted subsegments can be merged back into the original
segment.
- And the original segment will be sorted too.
Merging
- Scan from left to right, copying the minimum value.
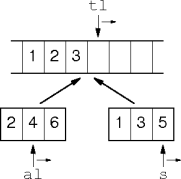
|
|
merge(T *
tl, tr, al, am, ar)
T * s = am
while tl < tr
if (al < am) ∧
(s == ar or *al < *s)
*tl++ = *al++
else
*tl++ = *s++
|
Mergesort
mergesort(T * aleft, aright, tleft, tright)
int len = aright - aleft
if len > 1
int h = len/2
T * amid = aleft + h
T * tmid = tleft + h
mergesort(aleft, amid, tleft, tmid)
mergesort(amid, aright, tmid, tright)
merge(
tleft, tright, aleft, amid, aright)
Performance
- The extra copying extracts a run-time cost.
Caveat Emptor
- What does O(n) extra space buy?
Some Problems
- AT&T handles about a billion phone calls per day.
- They all need to be recorded.
- How do you do it?
- The U.S. Post Office handles about
580 million pieces of mail a day.
- They all need to be routed.
- How do you do it?
The Big Idea
- In both cases, the keys are fixed-length numbers.
- A key can be re-interpreted as a base-M number.
- M is the radix.
- Two common values are M = 2i, i > 0, and M =
10.
- The key is decomposed into radix-M digits.
A Radix-10 Example
- To sort a set of three-decimal-digit numbers:
- Sort the 100s: 000 to 099, 100 to 199, ...
- Sort each 100s group by 10s: 00 to 09, 10 to 19, ...
- Sort each 10s group by 1s: 0 to 9.
Radix Exchange Sort
- The previous example with radix-2 digits (binary) is called
radix exchange sorting.
- With only two digits, radix exchange sort is similar to quicksort.
- The partition segregates the ith 0 and 1 bits in the key.
Example Radix Exchange Sort

Radix Exchange Sort
re-sort(int * left, int * right, int bit)
// Place elements in [left, right)
// in increasing order.
if left + 1 < right and bit < 32
int * mid = partition(left, right, bit)
re-sort(left, mid, bit + 1)
re-sort(mid + 1, right, bit + 1)
Performance
- Given n b-bit keys, radix exchange sort does
- O(n) work for each partition, and
- O(b) partitions.
- Radix exchange sort does O(nb) worst-case work.
- This is more than O(n) but sometimes less than O(n log n).
- b is independent of n, but is not constant.
Oh Really?
- When b = 8, b < log2 n when n =
256,
but
when b = 64, b < log2 n when n >
1.8×1019.
The Last Step
- We still don't have a linear sort.
- Let's go back to the mail room. How does a mailroom sort mail?
- Each recipient has a mailbox.
- Each piece of mail is placed in the recipient's mailbox.
- This is a linear-time sort.
Requirements
- A linear-time sort has two requirements:
- Enough space to store the sorted values.
- A constant-time addressing scheme to locate values in the space.
- A sort meeting these requirements is known as a bucket (or
distribution) sort.
Data Structures
- An array meets the linear-sort requirements.
- Its size is equal to the number of elements being sorted.
- Indexing is a constant function of the values being sorted.
- Other data structures can also support linear-time searches.
Bucket Sort
- Assume 3-digit decimal numbers.
bucket_sort(int a[], int n)
int counts[1000]
for i = 1 to n
counts[a[i] + 1]++
int j = 1
for i = 1 to 1000
while counts[i]-- > 0
a[j++] = i - 1
assert(j == n)