Programming Assignment 7 - Order Distances

Advanced Programming I, Spring 2006

Due Date

This assignment is due by 5:30 p.m. on Tuesday, 2 May.

See the assignment turn-in page (last modified on 18 January 2006) for instructions on turning in your assignment.

A dual-queue distributed bus (DQDB) is network based on a pair of buses. Each bus is divided into an integral number of fixed-length slots moving down the bus at a fixed rate; the slots in each bus move in opposite directions.

a dqdb network

Computer A communicates to computer B by waiting until an empty slot passes A's network interface on the bus moving in the direction of B. When A detects an empty slot it writes a packet into the slot. The packet contains B's address, which is recognized by B's network interface as the slot passes; the packet is removed from the slot, emptying the slot. B can then communicate with A by repeating the process on the opposite bus.

A DQDB network works best when packets make short trips on the busses. This occurs when computers that usually communicate are close together in the network. This can be modeled with an undirected graph and the idea of order distances.

The vertices of a graph G represent computers on the same DQDB network. An undirected edge between two nodes indicate computers that communicate with each other frequently.

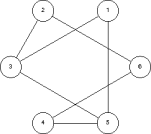
example communications graph

The graph vertices can be arranged in a linear order to represent the computer's ordering on the network.

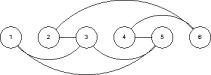
example linear ordering

The order distance of a vertex v in such an arrangement is the largest number of nodes between v and any of v's neighbors. Node 3 in the previous image has order distance 1, as does node 4. The order distance of G is the largest order distance of all the vertices in G. The graph in the previous image has order distance 3, the order distance of the vertices 1 and 6.

The Problem

Write a program that reads a graph description from std-in and writes to std-out a linear ordering of the graphs' vertices that minimizes the graph's order distance; the program should also output the graphs' minimal order distance.

Input

The input will be a graph in edge list form. Each non-blank line read describes a vertices's neighbors; each non-blank line read should have the form

v n₁ n₁ ... n_i

for 0 ≤ i. For example, the graph given in the Background Section would be specified by the input

Output

The output should be one line containing the minimal order distance found followed by the linear order of vertices:

d v₁ v₁ ... v_n

assuming the original graph had n vertices.

Testing

The program gen-graph in the assignment directory /export/home/class/CS-503/a7 writes to std-out a description of an undirected graph in the format expected by your program.

This page last modified on 27 April 2006.