Advanced Programming I Lecture Notes

4 April 2006 • Hashing Basics

Outline

• Arrays again.

• Hash tables.

• Hash functions.

• Hash table ADTs.

• Open-address hashing.

  • Collisions, linear and quadratic probing, double hashing.

• Chaining

Arrays Again

• Arrays provide O(1)-time access and no-overhead storage.

• However, finding values in an array can be expensive.

  • It can take O(log n) or O(n).

  • O(log n) search makes value access more expensive.

• There's no relation between a value and its index.

An Idea

• Suppose a value could be uniquely associated with an index.

• Then searching would also be constant time.

  • Is "joe" around?

  • Oh, "joe"'s the same as 2.

  • a[2] == "joe".

• This is the basic idea behind hash tables.

Hash Table Properties

• A hash table is an array-like data structure for storing and retrieving data.

• Constant-time data access and search.

  • And the constant should be close to one.

• Other array-like properties may be sacrificed for the constant-time operations.

  • Ordered sequential access, for example.

• Even so, constant-time operations may be elusive and expensive to achieve.

Hash Table Components

• A hash table comprises two parts:

  1. A hash function to map values to indices.

  2. A scatter (or hash) table to map indices to values.

• Both parts are sensitive to value characteristics.

  • Hash functions to the content of values.

  • Scatter tables to the number of values.

• These sensitivities complicate hash tables.

Hash Functions

• A record is identified with one or more fields collectively called the key.

• A hash function maps keys into a smaller range of positive integers (hash indices).

  • Smaller relative to the key set.

• The hash function may be supplied by the hash-table ADT, or by the ADT's client, or by both.

Hash-Function Properties.

• A hash function is a function.

  • That is, if k₁ = k₂, then h(k₁) = h(k₂).

• A good hash function is one that

  • produces unpredictable hash indices (is random).

  • produces widely and evenly separated hash indices (is uniform).

  • is fast to compute (is efficient).

Hash-Function Properties..

• A hash function maps a large key set to a much smaller index set.

  • All possible strings into 32-bit integers.

• By the pigeon-hole principle, many values will be mapped into the same hash index.

  • Dealing with this is a main concern of hash-table ADTs and their clients.

• Other properties may be important on occasion.

Finding Hash Functions

• A key can be interpreted as a large binary number.

  • Use multi-precision arithmetic to chop it down.

• Structured keys lead to recursive hash functions.

  • Use a hash function on each component, then hash together all the hash indices.

Hash Table ADTs

• Start with the usual three operations: add(), remove(), and find().

• There will be others to come, particularly maintenance operations.

• There may or may not be traversal operations.

  • There definitely won't be ordered traversal operations.

ADT Implementation

• There are two parts: the hash function and the scatter table.

  • For the moment, assume the hash function exists.

• The scatter table stores values and maps hash indices to values.

• The scatter table is most naturally based on an array.

Open-Address Hashing

• Implementing a hash table with an array results in open-address hashing.

• The array is arranged in B buckets, each containing b array elements.

  

  • B and b are parameters to the create() operator.

  • Assume B = N and b = 1.

Collisions

• Two keys collide when they produce the same hash index.

  • Collisions are guaranteed.

• How do you know when an array element is occupied?

  • The ADT includes an N-element bit vector to keep track.

  • Or have an otherwise unused sentinel value.

Handling Collisions

• Handling collisions involves storing the new value elsewhere in the hash table.

  If h(k) is full, examine (h(k) + 1) % N, then (h(k) + 2) % N, then ..., (h(k) + N - 1) % N.

• This is linear probing.

Linear-Probing Example

Handling Clustering

• Linear probing leads to clustering.

  

• Quadratic probing spreads out successive probes.

  • (h(k) + i²) % N for 0 ≤ i < N.

Quadratic-Probing Example

Double Hashing

• Quadratic probing is still predictable, leading to secondary clustering.

  • Although the clusters are smaller.

• Double hashing (rehashing or quotient-offset hashing) uses a second hash function to add unpredictability.

  • Visit (h₁(k) + u*i) % N
    for 0 ≤ i < N and u = h₂(k).

Double-Hashing Example

Problems

• Scatter tables under open addressing

  • may get full.

  • may have long searches due to clustering.

Chaining

• Let each bucket in the scatter table be the head of a linked list.

• Elements hashing to a bucket are added to the associated list.

  • No more clustering.

  • The table can hold an arbitrary number of elements.

    • At increasingly bad performance.

• This technique is known as chaining.

Chaining Example

Coalescing

• Open addressing imposes clustering costs; chaining imposes storage-management costs.

• Split the difference by reserving some buckets as chain links.

  • Chain management is cheap and fast.

  • Collisions don't cause clustering.

• The result is coalesced hashing.

Coalescing Implemented

• The number of overflow buckets is a design or run-time parameter.

• A free list chains unused overflow buckets.

  • Or use the occupied bit vector at linear cost.

Private ADT Operations

• Implement add(), remove(), and find().

• They use the locate() private operation.

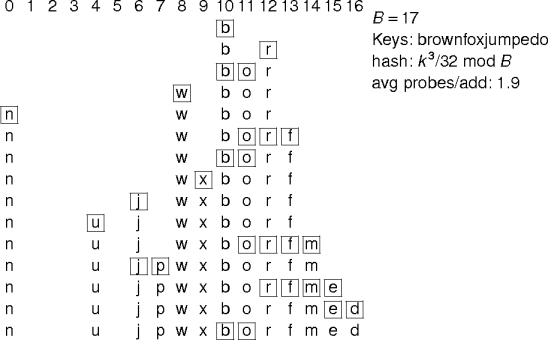
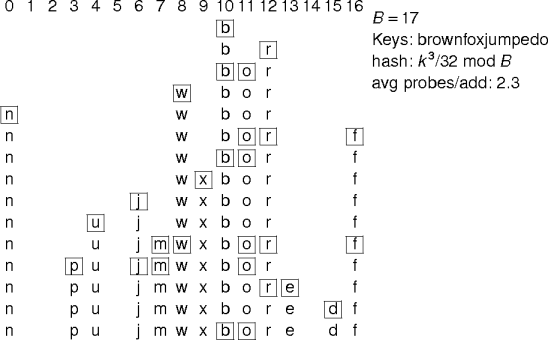
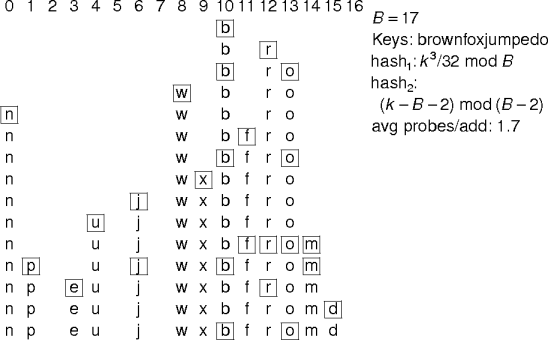
  bool locate(key k, int & hi)
    hi = hash(k)
    u = 1 or i2 or hash2(k)
    for i = 1 to B
      if not occupied[hi] return false
      if table[hi] == k return true
      hi = (hi + u) mod B
    hi = -1
    return false
  

Public ADT Operations

void add(key k)
  if not locate(k, hi)
    if hi > -1
      table[hi] = k
      occupied[hi] = true

void remove(key k)
  if locate(k, hi)
    occupied[hi] = false

bool find(key k)
  return locate(k, hi)

Implementation Details

• Two important implementation details are

  1. hash-table size (the value of B), and

  2. the hash functions.

Hash Function Issues

• Some important details for hash-function implementation include:

  1. How are they created?

  2. Who provides them?

  3. How good are they?

Hash Function Mechanics

• A hash function maps arbitrary data (the key) into a small range of integers (the hash-table indexes).

• This can be divided into two steps:

  1. Reduce the key to an integer

  2. Reduce an integer to a hash-table index.

Keys To Integers

• The key-to-integer mapping is data dependent, but has the general form:

  • Treat the key as a sequence of n-byte values for n ∈ { 1, 2, 4, 8 }.

  • Use arithmetic to combine the values into a single value.

• There may be other techniques, such as use the key address.

Hash Functions

• Hash functions fall into one of three classes based on value combination:

  • Multiplication based, division based, or bit-twiddling based.

  • There are also other techniques.

• Random-number generation is a closely-related area.

  • For implementations and evaluations.

Hashing by Bit Twiddling

• Create rp[], a random permutation of the 256 integers 0 to 255 (byte values).

• Given a sequence v[] of n byte values, hash v into a byte value h with

  byte hash(byte v[], unsigned n)
    byte h = rp[v[0]]
    for i = 1 to n - 1
      h = h xor rp[v[i]
    return h
  

• Combining several values from hash() produces multi-byte hash values.

Hashing by Division

• This is the typical hash function.

  unsigned hash(unsigned k)
    return k mod B
  

  • B is the bucket count, and "should be prime."

• Linear congruential generators are a variation.

  unsigned hash(unsigned k)
    return (M*k + a) mod B
  

  • This is overkill, most likely.

Hashing by Multiplication

• Hashing by multiplication uses functions of the form

  unsigned hash(unsigned k)
    return floor(B*fraction(k*A))
  

  • A is any value and B need not be prime.

Comments

• Random-permutation hashing is fast, reliable, simple, and general purpose.

  • The key is generating a random permutation, which is easy.

• Multiplication- or division-based hashing is less fast, less reliable, less simple, and less general purpose than random-permutation hashing.

  • Real arithmetic is expensive, and getting the parameters correct is tricky.

Hash Function Sources

• Hash functions can be provided by the ADT, the ADT client or both.

  • There may be other sources, such as a language run-time or a VM.

• The client knows about the data; the ADT knows about the hash table.

  • Good hash functions needs to know about both.

ADT Hash Functions

• A hash-table ADT has

Client Hash Functions

• These are mainly key-to-integer mappings.

Dual Hash Functions

• Not deciding is a good strategy: have the client and ADT each provide a hash function.

  • The final hash is h_A(h_C(k)).

• Each side can exploit its strengths without bothering the other side.

• The ADT can change its hash function without customer coordination.

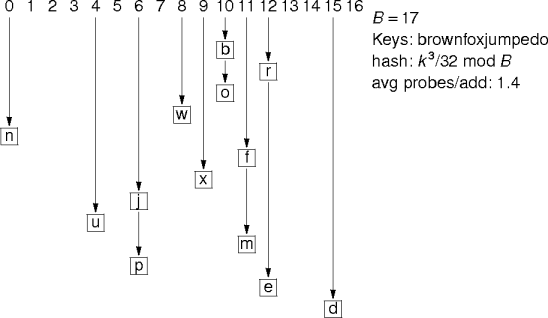
Evaluating Hash Functions

• A good hash function should generate indices that are uniformly and randomly distributed over the buckets.

• There are mathematical (statistical) tests for evaluating randomness.

• A simpler alternative is to plot the hash function and look for patterns.

  • Patterns can indicate non-uniformity and non-randomness.

Example.

Example.

References

• Hashing, Section 6.4 in The Art of Computer Programming, Vol. 3: Sorting and Searching by Donald Knuth, Addison-Wesley, 1973.

• Hash Tables by Pat Morin, Chapter 9 in Handbook of Data Structures and Algorithms, edited by Dinesh Metha and Sartaj Sahni, Chapman & Hall/CRC, 2005.

• Hashing, Chapter 9 in Algorithms by Robert Sedgewick, Addison-Wesley, 1983.