Lecture Notes for Simulation

24 January 2005 - Simulation

Systems

• A system is a collection of entities exchanging events in reaction to stimuli.

• Reasons for analyzing systems:

  • Altering behavior to make the system operate with less noise or fewer resources (optimization).

  • Forecasting behavior to speculate how changes may affect the system.

  • Analyzing behavior to determine which and how system part combine to produce a paritcular result.

  • Comparing behavior among several similar systems.

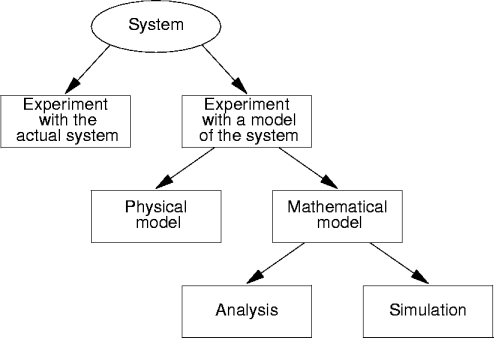
System Analysis

• There are various analysis techniques that can be applied to systems.

Simulation Types

• Static vs. dynamic.

  • Static: the model is unchanging.

  • Dynamic: the model changes over time.

• Deterministic vs. stochastic.

  • Deterministic: output is (eventually) predictable given the inputs.

  • Stochastic: output is never exactly predictable.

• Continuous vs. discrete (global vs. local).

  • Discrete: changes occurs over a limited number of intervals.

  • Continuous: Change occurs over arbitrary intervals.

Simulation Types

• The model type influences the simulation type.

  • Fluid flow; continuous simulations.

    • Many independent interacting particles; differential models.

  • Instutional money flow; Hybrid discrete-continous simulations.

    • Discrete agents with continuous cumulative attributes.

  • The area of a circle; Monte Carlo simulations.

    • Analytically intractable, static models.

Discrete-Event Models

• A discrete-event model

  • evolves over time (is dynamic) and

  • changes instaniously at identifiable times (is discrete).

  • It may be stochastic or deterministic.

• The system being modeled need not have these properties.

Example Discrete-Event Model

• How long does someone wait in line at a single-ATM booth?

• Model entities: the ATM, the queue, customers.

• Model events: Customers join or leave the queue, a customer starts and finishes using the ATM.

  • If customers don't get disgusted and leave before service, The customer starts ATM and customer leaves queue are the same.

• Model parameters: customer arrival rate, customer service rate.

• Simple versions of this model have closed-form (analytic) solutions via queuing theory.

  • However, the model easily becomes non-simple.

Discrete-Event Simulation

Single Server Queue Example

Simulation Advantages

• Often the most partical way of dealing with complex, dynamic, stochastic systems.

• Changing the simulation can be easy, allowing for what-if experimentation.

• Normally uncontrollable factors, such as time and environment, are controlled in a simulation.

Simulation Disadvantages

• Simulations can never provide answers, they can only suggest them.

  • But a good simulation make strong suggestions.

• Developing or using simulations may be expensive.

• The validity and verasity of simulations and are always under question.

  • Time is the only cure for this (but systems evolve).

This page last modified on 25 February 2005.