<main()>=
int
main(int argc, char * argv[]) {
cl_options opts;
opts['e'] = "0.005";
get_cl_options(argc, argv, opts);
epsilon = atof(opts['e']);
points pts;
<read the input>
<find and output the polygons>
}
Defines main (links are to index).
Used below.
<read the input>=
std::copy(std::istream_iterator<point>(std::cin),
std::istream_iterator<point>(),
std::inserter(pts, pts.end()));
if (not std::cin.eof()) {
std::cerr << "! Input error while reading pts.\n";
return EXIT_FAILURE;
}
Used above.
Following the output order, look for triangles first, then squares, and so on
up to the number of points input.
<find and output the polygons>=
for (unsigned i = 3; i <= pts.size(); i++) {
polygons rpolys;
find_rpolys(pts, rpolys, i);
if (not rpolys.empty()) {
std::cout << i << "\n";
std::copy(rpolys.begin(), rpolys.end(),
std::ostream_iterator<polygon>(std::cout, "\n"));
}
}
Used above.
Extracting points from the input stream seems a bit complicated, so it might be
worth while trying to figure out why it must be so.
<point extraction>=
static std::istream &
operator >> (std::istream & is, point & pt) {
// Read from the given input stream a point and store it in the given
// reference.
is >> pt.x;
if (is.good()) {
is >> pt.y;
if (not is.good())
is.clear((is.rdstate() & ~std::ios::eofbit) | std::ios::failbit);
}
return is;
}
Used below.
At first glance, the much simpler
return in >> pt.x >> pt.y;
would seem to do the trick, but this code has a problem: it doesn't distinguish
between and end-of-stream that occurred while reading the x coordinate - which
is legal and indicates the end of input - from an end-of-stream that occurs
when reading the y coordinate, in which the missing coordinate causes a format
error. To make such a distinction, the code has to read the coordinates in two
parts, with an error check between.
The second source of complexity comes about from making sure the stream returns
the proper error status. As shown by <read the input>, the expected
input behavior is to fail at the eof when all the points have been read; that
is, the eof failure is normal and indicates that nothing is wrong.
The eof that occurs when trying to read the y coordinate should not be taken as
a normal eof, but as an error; this is why the eof bit is cleared. Although
it's most likely true that some other status bit was also set at the premature
end-of-stream (probably the fail bit to indicate a format error), explicitly
setting the fail bit will make sure this is true.
Testing between coordinate reads and clearing the eof bit lets the point
extractor indicate that input with an odd number of coordinates is illegal.
The cascaded input is >> pt.x >> pt.y can't make the same indication given
the ambiguity over when the eof occurred.
<main.cc>=
#include <algorithm>
#include <iterator>
#include <iostream>
#include <cstdlib>
#include "cl-options.h"
#include "rpoly.h"
#include "find-rpolys.h"
<main()>
<point extraction>
Defines main.cc (links are to index).
This code is written to a file (or else not used).
How do you find the regular polygons in a set of points? Exhaustive search
could work: to find i-sided regular polygons, check all subsets of i
points to see if they form a regular polygon. This is simple and obviously
correct, but it ignores a lot of geometric information that we can exploit to
provide a more efficient search.
Given a set of n > 2 points, pick any two points from the set. These two
points could form one side of an i-sided regular polygon. To determine if
they do, we could find the other i-2 points in the polygon and see if
those points are in the set too. If they are, then we've found an i-sided
regular polygon.
The previous paragraph provides the basis for implementing the
search_poly() procedure that looks for an i-sided regular polygon
given a side. The point set is specified as an iterator range that does not
contain the two points forming the side; this simplifies the serach for the
candidate polygon in the point set.
<searching for a polygon>=
static void
search_poly(
const point & p1, const point & p2, unsigned sides,
const pts_citer & begin, const pts_citer & end,
polygons & polys) {
// Look in the given point set [begin, end) for a polygon of the given size
// having the given line segment as a side; store any such polygon found
// in the given reference.
polygon poly;
gen_poly(poly, p1, p2, sides);
polygon sorted_poly(poly);
std::sort(sorted_poly.begin(), sorted_poly.end());
polygon match;
std::set_intersection(sorted_poly.begin(), sorted_poly.end(),
begin, end,
std::back_inserter(match));
if (match.size() + 2 == sides)
polys.push_back(poly);
}
Defines search_poly (links are to index).
Used below.
The search for the candidate polygon is performed by intersecting the set of
points with the set of candidate polygon vertices and making sure there's
enough common points. This is not the most efficient way to go, but it is
clear and simple.
There's a couple of ways to find a i-sided regular polygon given a side.
Probably the simplest way is to pick one of the two given points as a pivot
point and then rotate the other point about the pivot until it co-incides with
another vertex in the polygon. The new vertex becomes the pivot point and the
rotations are repeated until all the vertices are placed.
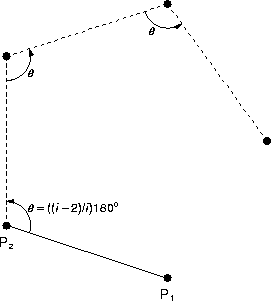
The pivoting-side method for generating a candidate polygon is not the best
approach because the positional inaccuracies accumulate in each successive
vertex and are magnified by each rotation. A more numerically stable approach
finds the center of the candidate polygon and rotates one (or both) of the
given points once into each new vertex position, which minimizes both the
initaial and accumulated errors.
However, the pivoting-side approach works
well enough and is relatively simpler than finding the polygon's center.
Because an edge can belong to two polygons (one on either side of the edge),
the two points defining the edge are oriented from the first to the second.
<create a candidate polygon>=
static void
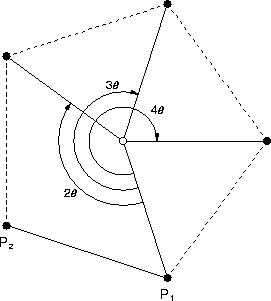
gen_poly(polygon & poly, const point & p1, const point p2, unsigned sides) {
// Generate a regular polygon having the given number of sides and given line
// segment as one of the sides; store the polygon in the given point-set
// reference. The polygon's inside is to your right as you walk from p1 to
// p2.
assert(sides > 2);
const double angle = (static_cast<double>(sides - 2)/sides)*pi;
poly.push_back(p1);
poly.push_back(p2);
for (unsigned i = 2; i < sides; i++)
poly.push_back(rotate(poly[i - 2], poly[i - 1], angle));
}
Defines gen_poly (links are to index).
Used below.
With all the previous machinery in place, finding all i-sided regular
polygons in a given set of points is simple: consider each pair of points as an
edge and then find all polygons from that edge (correctly manipulating the
bidirectional set iterators is a bit of a pain, though). The candidate points
are considered in both orders to make sure both sides of the edge are examined.
<finding polygons>=
void
find_rpolys(const points & pts, polygons & polys, unsigned sides) {
polys.clear();
for (pts_citer i = pts.begin(); i != pts.end(); ++i) {
pts_citer j = i;
for (++j; j != pts.end(); ++j) {
pts_citer k = j;
search_poly(*i, *j, sides, ++k, pts.end(), polys);
search_poly(*j, *i, sides, k, pts.end(), polys);
}
}
}
Defines find_rpolys (links are to index).
Used below.
The double loop takes O(n2) time for n points, and
search_poly() takes O(n) time on each call, for a total of
O(n3). There's lots of geometric information that isn't being
exploited in this solution, so it's quite possible that there's an
asymptotically better solution than this one; but for now, this will do..
<find-rpolys.cc>=
#include <algorithm>
#include <cmath>
#include <iostream>
#include <cassert>
#include "find-rpolys.h"
#include "rpoly.h"
// what pi is.
const double
pi = M_PI,
two_pi = 2*pi;
// Deja vu c++ style.
static void search_poly(const point &, const point &, unsigned,
const pts_citer &, const pts_citer &, polygons &);
static point rotate(point, const point &, double);
<finding polygons>
<create a candidate polygon>
static point
rotate(point p1, const point & p2, double angle) {
// Rotate the point p1 about the point p2 through the given angle; return the
// rotated point.
point p;
const double
cos_a = cos(angle),
sin_a = sin(angle);
p.x = p1.x - p2.x;
p.y = p1.y - p2.y;
p1.x = cos_a*p.x - sin_a*p.y;
p1.y = sin_a*p.x + cos_a*p.y;
p1.x += p2.x;
p1.y += p2.y;
return p1;
}
<searching for a polygon>
#ifdef FRTESTING
// g++ -o frtesting -DFRTESTING -ansi -pedantic -Wall -g find-rpolys.cc rpoly.cc && ./frtesting
int main() {
point p1, p2, p3;
p1.x = 1;
p1.y = 1;
p2.x = 2;
p2.y = 1;
p3 = rotate(p1, p2, pi/2);
assert(equal(p3.x, 2));
assert(equal(p3.y, 0));
p3 = rotate(p2, p1, pi/2);
assert(equal(p3.x, 1));
assert(equal(p3.y, 2));
p1.x = 1;
p1.y = 1;
p2.x = 2;
p2.y = 2;
for (unsigned i = 3; i < 20; i++) {
polygon poly;
gen_poly(poly, p1, p2, i);
p3 = rotate(poly[i - 2], poly[i - 1], (static_cast<double>(i - 2)/i)*pi);
assert(equal(p3.x, poly[0].x));
assert(equal(p3.y, poly[0].y));
}
}
#endif
Defines find-rpolys.cc (links are to index).
This code is written to a file (or else not used).
<rpoly.h>=
#ifndef _rpoly_h_defined_
#define _rpoly_h_defined_
#include <set>
#include <vector>
#include <ostream>
// What a point is. You can't use std::pair because istream iterators freak
// out when extracting std::pairs in g++.
struct point { double x, y; };
// A set of points.
typedef std::set<point> points;
typedef points::const_iterator pts_citer;
// A polygon.
typedef std::vector<point> polygon;
// A set of polygons.
typedef std::vector<polygon> polygons;
// Return true iff the given values are (close enough to being) equal.
extern bool equal(double, double);
// The less-than operator for points.
extern bool operator < (const point &, const point &);
// Write the given point to the given output stream.
extern std::ostream & operator << (std::ostream &, const point &);
// Write the given polygon to the given output stream.
extern std::ostream & operator << (std::ostream &, const polygon &);
// What "close enough" means.
extern double epsilon;
#endif
Defines rpoly.h (links are to index).
This code is written to a file (or else not used).
<rpoly.cc>=
#include "rpoly.h"
#include <cmath>
#include <ostream>
#include <iterator>
#include <iomanip>
// How close is "close enough"?
double epsilon = 0.0001;
// Deja vu c++ style.
static std::ostream & outv(std::ostream &, double);
bool
equal(double d1, double d2) {
return fabs(d1 - d2) < epsilon;
}
static bool
less(double d1, double d2) {
// Return true iff d1 is close enough to being less than d2.
return (d1 - d2) < -epsilon;
}
bool
operator < (const point & p1, const point & p2) {
return less(p1.x, p2.x) or (equal(p1.x, p2.x) and less(p1.y, p2.y));
}
std::ostream &
operator << (std::ostream & os, const point & pt) {
return outv(outv(os, pt.x) << " ", pt.y);
}
std::ostream &
operator << (std::ostream & os, const polygon & pg) {
std::copy(pg.begin(), pg.end(),
std::ostream_iterator<point>(os, " "));
return os;
}
static std::ostream &
outv(std::ostream & os, double v) {
// Output the given value to the given otput stream; return the stream.
return os << std::fixed << std::setprecision(3) << v;
}
#ifdef RPTESTING
// g++ -o rptesting -DRPTESTING -g -ansi -pedantic -Wall rpoly.cc && ./rptesting
int main() {
point p1, p2;
p1.x = 1;
p1.y = 1;
p2.x = 1;
p2.y = 2;
assert(p1 < p2);
assert(not (p2 < p1));
}
#endif
Defines rpoly.cc (links are to index).
This code is written to a file (or else not used).

