// Read in the strokes. // Classify the strokes into nodes and edges. // ? // Group the nodes and edges into a tree. // Make the tree tidy. // Output the tree.
Your colleague would like to replace the question mark ? with an assertion
that will fail if the collection of nodes and edges cannot be combined into
into a tree.
Note that the assertion should determine if the nodes and edges cannot be formed into a tree. The assertion should not determine if the nodes and edges can be formed into a tree (which is probably not possible to do in an assertion).
What assertion do you recommend that your colleague use? Your answer should be
in the form of a valid assert() statement, with an explanation of why the
assertion works.
One useful assertion is
assert((node_count + edge_count == 0) or (edge_count + 1 == node_count))
This assertion exploits the property that a valid tree has one more node than
it has edges. It also takes care of the case when input is empty (assuming
node_count and edge_count are unsigned integers) .
Most people either got this or they got it completely wrong, although one person offered up the assertion
assert((nodes && edges) == tree);
which would be lovely if you could do it.
{
init-statement
while (condition) {
statement;
expression
}
}
is equivalent to the for statement
for(init-statement; condition; expression) statement
Your colleague believes that the outer-most pair of brackets is unnecessary and the code
init-statement
while (condition) {
statement;
expression
}
works just as well as the code given by Koenig and Moo.
Do you agree or disagree with your colleague? If you agree, explain why the outer-most pair of braces is not needed. If you disagree, give an example of where your colleague's replacement code is not equivalent to a for statement.
You should disagree with your colleague. The outer pair of brackets creates a new scope for any index variables declared, which avoids potential name clashes. For example, your colleague would translate the following valid C++ code
int i; for (int i = 0; i < 10; i++) // whatever
into the clearly invalid
int i;
int i = 0;
while (i < 10) {
// whatever
i++
}
while Koenig and Moo would translate it into the valid
int i;
{int i = 0;
while (i < 10) {
// whatever
i++
}
}
Most people got this one, although the degree to which people showed an understanding of the scope issues varied widely.
Write the developer's function.
You need one fence post to start. To use the minimum number of fence posts, put a fence post at the end of every 3 meter segment, the maximum distance allowed between fence posts. There are n/3 such segments, where n is the length of the fence in meters. Finally, you may need need one more fence post to take care of any leftover if the fence length is not an integral multiple of 3.
The previous analysis leads straightaway to the code
unsigned fence_posts(int fence_length) {
const unsigned meters_between_posts = 3;
if (fence_length < 1)
return 0;
else
return 1 + fence_length/meters_between_posts +
(fence_length % meters_between_posts > 0 ? 1 : 0);
}
This code can be simplified slightly by using the ceiling function:
unsigned fence_posts(int fence_length) {
const double meters_between_posts = 3.0;
if (fence_length < 1)
return 0;
return 1 + static_cast<unsigned>(
std::ceil(
static_cast<double>(fence_length)/meters_between_posts));
}
A lot of people missed this question, which is terrible. The errors were evenly divided among people who forgot the 1 for the initial post and forgot the 1 for whatever was left over after all the 3-meter segments (and the few people who forgot both).
As a historical note, this is why off-by-one errors are sometimes called fence-post errors: How many fence posts will I need for a 100 foot fence with a fence post every 10 feet?
tstroke, no need to numerically describe the strokes.
A sketch like
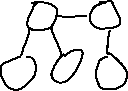
will do the trick. If the program makes the left node the root, the resulting tidy tree looks like
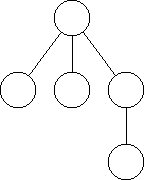
while if it picks the right node to be the root, the resulting tidy tree looks like
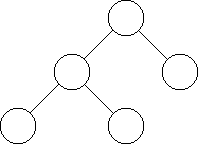
A lot of people answered this question by sketching input that wasn't a valid tree. In addition to making it unclear how such input could answer the question in theory, the program should reject such input as invalid, which makes it impossible to answer the question in practice.