Given the set of colored points pts and the sequence of clear points
indicated by the iterator range (b, e), partition the iterator range
(b, e) so that all points inside a triangle defined by three points in
pts precede all points that do not fall within a triangle made from any
points in pts. Return an iterator to one past the in-triangle clear
points (that is, return an iterator to the start of the non-in-triangle
clear points).
<es-tri procedures>=
static ptvec_iter
tri(const ptvec & pts, ptvec_iter b, ptvec_iter e) {
if (pts.size() >= 3)
for (ptvec_citer i = pts.begin(); i != pts.end() - 2; i++)
for (ptvec_citer j = i + 1; j != pts.end() - 1; j++)
for (ptvec_citer k = j + 1; k != pts.end(); k++)
if (!collinear(*i, *j, *k))
b = std::partition(b, e, in_triangle(*i, *j, *k));
return b;
}
Definestri(links are to index).Used below.
As should be clear from the code, this is an O(n4) algorithm.
The only other tricky bit for this solution is determining if a point is in or out of a triangle. There's lots of ways to determine if a point is in a triangle, but one of the easier and more efficient ways is based on the notion of a turn.
If you walk around the perimiter of a triangle, a point inside the triangle will always be to your left or to your right. If you spot a point that's sometimes on your left and sometimes on your right, then it can't be a point in the triangle. (If you think about it, you'll see there's a small problem with this property: what happens when the point is on the triangle's perimiter? This turns out to be not a big problem, because you can restate the propery as "if the point is never to your left when walking clockwise or to your right when walking counterclockwise, then the point's in the triangle.")
Now all that's needed is a way to determine if a point's on the left or right of a line. Given three points, imagine you're walking from the first to the third point via the second point. At the second point, you have to do one of three things: turn to the left (or counter-clockwise), turn to the right (or clockwise), or not turn at all (not turning assumes you can walk backwards).
A turn can be calculated easily from line slopes; a left turn goes from a line of smaller slope to a line of larger slope and a right turn goes from a line of larger slope to a line of smaller slope. A little algebra removes the danger of misbehaved denominators to give the function
<turn function>=
int turn(const point & b, const point & m, const point & e) {
// Return -1 if you have to turn left at point m when traveling from
// point b to point e. Return 1 if you have to turn right at point m
// when traveling from point b to point e. Return 0 if you don't turn
// at point m when traveling from point b to point e.
const int i = (e.first - b.first)*(m.second - b.second) -
(m.first - b.first)*(e.second - b.second);
return (i > 0) ? 1 : ((i < 0) ? -1 : 0);
}
Definesturn(links are to index).Used below.
Given turn(), the in-triangle predicate is simple, except for one
complication: given the arbitrary points v1, v2, and v3, it's
unclear whether walking from v1 to v2 to v3 is going clockwise or
counter-clockwise. Rather than figure it out, the in-triangle predicate uses a
bit more complicated test on the turns.
<in-triangle predicate>=
bool operator () (point p) {
// Return true iff point p is in or on the triangle (v1, v2, v3).
const int
t1 = turn(v1, v2, p),
t2 = turn(v2, v3, p),
t3 = turn(v3, v1, p);
// If i = 3, p is inside the triangle; if i = 2, p is on on an edge
// but not a vertex.
const unsigned i = abs(t1 + t2 + t3);
if ((3 == i) or (2 == i))
return true;
// If two of the three turns is zero, the p coincides with a vertex,
// otherwise p is outside the triangle.
return ((0 == t1) and (0 == t2)) or
((0 == t2) and (0 == t3)) or
((0 == t3) and (0 == t1));
}
Definesturn(links are to index).Used below.
As the in-triangle prediate suggests, the in-triangle test is implemented as a functor. By defining a triangle struct, it could also be implemented as a binary prediate, but defining it as a functor makes it possible to hide the turn function as a private member.
<in-triangle functor>= class in_triangle { public: in_triangle(const point & v1, const point & v2, const point & v3) : v1(v1), v2(v2), v3(v3) { } <in-triangle predicate> private: // The triangle virtices. const point & v1, & v2, & v3; <turn function> };
Definesin_triangle(links are to index).Used below.
After the in-triangle functor, everything else is relatively straighforward.
<es-tri.cc>=
#include <algorithm>
#include <iostream>
#include "triangulations.h"
// Deja vu, c++ style.
static double delta(int, int);
static double dabs(double);
// What "close enough" means.
const double epsilon = 0.00001;
<in-triangle functor>
static bool
collinear(const point & v1, const point & v2, const point & v3) {
// Return true iff the given points lie on the same line.
return dabs(delta(v1.second, v2.second)*delta(v1.first, v3.first) -
delta(v1.first, v2.first)*delta(v1.second, v3.second)) < epsilon;
}
static double
delta(int i, int j) {
// Return the distance between i and j.
return static_cast<double>(i - j);
}
static inline double
dabs(double d) {
// Return the absolute value of the given value.
return d < -epsilon ? -d : d;
}
<es-tri procedures>
points
triangulations(const points & pts) {
points ans;
ans.c = pts.c;
const ptvec_iter
b = ans.c.begin(),
e = ans.c.end(),
g = tri(pts.g, b, e),
y = tri(pts.y, g, e);
ans.g.assign(b, g);
ans.y.assign(g, y);
ans.c.assign(y, e);
return ans;
}
#ifdef TESTING
// g++ -o tri-test -gstabs -ansi -pedantic -Wall -DTESTING es-tri.cc && ./tri-test
#include <cassert>
int main() {
const point p00(0, 0), p04(0, 4), p40(4, 0), p11(1, 1), p44(4, 4),
p12(1, 2), p21(2, 1);
assert(!in_triangle(p00, p44, p40)(p04));
assert(!in_triangle(p00, p44, p04)(p40));
assert(!in_triangle(p00, p11, p40)(p44));
assert(in_triangle(p00, p44, p40)(p00));
assert(in_triangle(p00, p44, p40)(p44));
assert(in_triangle(p00, p44, p40)(p40));
assert(in_triangle(p00, p44, p40)(p11));
assert(in_triangle(p00, p44, p40)(p21));
assert(!in_triangle(p00, p44, p40)(p12));
assert(!in_triangle(p00, p44, p04)(p21));
assert(in_triangle(p00, p44, p04)(p12));
}
#endif
Defineses-tri.cc(links are to index).This code is written to a file (or else not used).
Non-triangle points must be outside the cloud of colored points, so this sounds like a promising approach because it means attention can be focused on the edge of the cloud, ignoring all the points - colored and clear - inside the cloud. Now all we need is a way to find the clear points outside the cloud.
One simple observation to make is that if ymin is the smallest y coordinate of any colored point, then any clear point with a y value less than ymin must be outside the cloud. Although you can repeat the same observation with the other extreme coordinate values, that turns out not to be too helpful because it does nothing about the clear points outside the cloud but inside the bounding box.
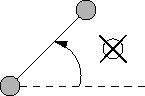
To make further progress, imagine a horizontal line through the colored point with the smallest y value (if there's more than one such point, take the rightmost one); call the point the pivod point. Now rotate the half-line to the right of the pivot point counter-clockwise until it hits another colored point. Here's the key observation: any clear points hit by the rotating line before it hits the colored point must be outside the cloud.

Now the rest of the algorithm should be clear: make the colored point hit by the rotating half-line the new pivot point and continue the rotation around the new pivot point as described in the previous paragraph. Keep rotating and selecting new pivots until the original pivot gets selected again. All clear points hit by the rotating line are outside the cloud, and, contrarewise, all clear points not hit by the line are inside of some triangle of colored points.
As with most geometric algorithms, the devil is in the details. But, before going on to consider the details, it might be a good idea to estimate the expected performance for this algorithm to see if we're on the right track. If it doesn't look good, we can drop it without having done too much work and try something to find something else.
Finding the minimal y colored point is linear. Finding the next pivot may have to look, in the worst case, at every other colored point, and so is linear. In the worst case every colored point may be a new pivot, which causes O(n2) behavior, where n is the total number of colored and clear points. O(n2) behavior is on the edge of respectible behavior, but it's certainly bettern than O(n4) behavior.
As describe above, and ignoring for a moment the details, the algorithm described above is easily implemented. First, find the initial pivot point.
<find the first pivot>= const point first_pivot = *std::min_element(pts.begin(), pts.end(), pivot_less); point current_pivot = first_pivot;
Definescurrent_pivot,first_pivot(links are to index).Used below.
In a loop, find the next pivot given the current pivot.
<find the next pivot>= const point next_pivot = sweep(current_pivot, current_angle, pts);
Definesnext_pivot(links are to index).Used below.
Knowing the current and next pivots, find the clear points hit while looking
for the next pivot and move them to the end of the iterator range (b,
e).
<find the outside clear points>= e = std::partition(b, e, keeper(current_pivot, current_angle, next_angle));
Used below.
If the next pivot is the first pivot, then the loop's done. Before breaking the loop, check the remaining clear points for hits.
<check for termination>=
if (first_pivot == next_pivot) {
e = std::partition(b, e,
keeper(next_pivot, next_angle, angle(360, 0)));
break;
}
Used below.
The tri() procedure implements the algorithm. The pivots variable
keeps track of the number of pivot points found; if less than three were found
(as would happen when all the colored points are collinear or are the same
point), there can be no triangles and all the clear points are outside.
<pivot and rotate>=
static ptvec_iter
tri(ptvec pts, ptvec_iter b, ptvec_iter e) {
// Partition the points in the given iterator range (b, e) so that points
// appearing in a triangle formed by three points from pts appear before the
// points that appear in no such triangle. Return an iterator to the first
// non-triangulated point.
if (pts.size() < 3)
return b;
<find the first pivot>
angle current_angle(0.0, 0);
unsigned pivots = 0;
while (true) {
<find the next pivot>
angle next_angle(current_pivot, next_pivot);
pivots++;
assert(pivots <= pts.size());
<find the outside clear points>
<check for termination>
current_pivot = next_pivot;
current_angle = next_angle;
}
return (pivots < 3) ? b : e;
}
Definestri(links are to index).Used below.
tri() makes use of angles to find the next pivot point and outside clear
points. In either case the angle of interest is the one the rotating line
makes with the x axis.
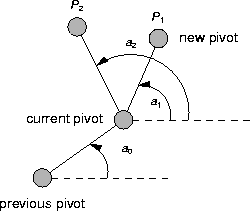
The next piviot is the colored point that forms the smallest angle (a1 in the previous figure) strictly larger than the angle used to select the current pivot (a0 in the previous figure).
<finding the smallest larger angle>=
static point
sweep(const point & pivot, const angle & min_angle, const ptvec & pts) {
// Search the given set of points and return the next pivot point, given
// current pivot point and the angle used to select the current pivot point.
point new_pivot;
std::for_each(pts.begin(), pts.end(),
min_pivot(pivot, min_angle, new_pivot));
return new_pivot;
}
Definessweep(links are to index).Used below.
This code has linear behavior, and, in the worst case, every point in pts
may be the current pivot, which gives the estimated O(n2) behavior.
The min_pivot functor used to find the next pivot point is elaborate
because of the number of arguments needed and also because it has to return the
next pivot point, which is done via an instance variable reference.
<the min-pivot functor>=
struct min_pivot {
// The current pivot point.
const point & pivot;
// The angle of the line (relative to the x axis) between the current
// point and the previous current point.
const angle & min_angle;
// The current best angle found.
// Invariant: 360 <= new_min_angle < min_angle
angle new_min_angle;
// The current best next point.
// Invariant: 360 < new_min_angle -> the line (pivot, new_pivot) forms
// an angle of new_min_angle with the x axis.
point & new_pivot;
min_pivot(const point & p, const angle & a, point & np)
: pivot(p), min_angle(a), new_min_angle(angle(360, 0)), new_pivot(np) {
new_pivot = p;
}
void operator () (const point & pt) {
// Determine if the given point is acceptable as the new next point in
// the convex hull.
if (pt != pivot) {
const angle a(pivot, pt);
if ((min_angle < a) and (a < new_min_angle)) {
new_pivot = pt;
new_min_angle = a;
}
}
}
};
Definesmin_pivot(links are to index).Used below.
Now it starts to get tricky. At first glance, it seems like the standard less-then binary predicate would serve as the ordering on angles. However, a second glance, at the figure below, shows that using just an angle causes problems when there are collinear points.
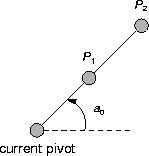
P1 and P2 both form angle a0 with the current pivot. When this happens, the point further away from the pivot should be the next pivot. (To understand why, imagine a clear point on the line between P1 and P2. If there's any other non-collinear colored point, then the clear point is in a triangle.)
With these observations, the definition of a < b for angles a and b is
<angle less-then>=
bool operator < (const angle & a) const {
return ((theta - a.theta) < -epsilon) or
((dabs(theta - a.theta) < epsilon) and
(((delta == 0) and (a.delta != 0)) or
(delta > a.delta)));
}
Used below.
The rest of the angle datatype is relatively straightforward. Note that we don't really care what the actual angle and distance values are; we only care about their relative magnitudes. The code below expliots this point by computing cheaper versions of the angle and distance measures.
<an angle>=
class angle {
public:
// Create the angle formed by the line (p1, p2) and the x axis.
angle(const point & p1, const point & p2) {
set(p1, p2);
}
// Create an angle from the given angle and distance.
angle(double t, unsigned d) : theta(t), delta(d) { }
// Reset this angle to be the angle formed by the line (p1, p2) and the x axis.
void set(const point & p1, const point & p2) {
theta = ang(p1, p2);
delta = lng(p1, p2);
}
<angle less-then>
// The angle (sorta) the line (p1, p2) makes with the x-axis.
double theta;
// The length (sorta) of the line (p1, p2).
unsigned delta;
private:
double ang(const point & p1, const point & p2) {
// Return the angle (sorta) between the line (p1, p2) and the x axis.
const int
dx = p2.first - p1.first,
dy = p2.second - p1.second,
d = abs(dx) + abs(dy);
double t =
(d == 0) ? 0.0 : static_cast<double>(dy)/static_cast<double>(d);
if (dx < 0)
t = 2 - t;
else if (dy < 0)
t += 4;
return t*90.0;
}
unsigned lng(const point & p1, const point & p2) {
// Return the length (sorta) of the line (p1, p2).
const int
dx = p2.first - p1.first,
dy = p2.second - p1.second;
return dx*dx + dy*dy;
}
};
Definesangle(links are to index).Used below.
Once the next pivot has been identified, all the clear points forming an angle between (inclusive) the old and new angles are outside points.
<inside points functor>=
struct keeper {
const point & pivot;
const angle & min_angle;
const angle & max_angle;
keeper(const point & p, const angle & na, const angle & xa)
: pivot(p), min_angle(na), max_angle(xa) { }
bool operator () (const point & pt) {
const angle a(pivot, pt);
const bool disposable =
(pt != pivot) and
((min_angle.theta <= a.theta) and
((a.theta < max_angle.theta) or
((a.theta == max_angle.theta) and (max_angle.delta < a.delta))));
return !disposable;
}
};
Defineskeeper(links are to index).Used below.
Because the first pivot has the smallest y value, the standard lexicographic less-then prediate defined on points (interger pairs) won't work and we need to define an alternative that does.
<minimal pivot less-than>=
static bool
pivot_less(const point & pt1, const point & pt2) {
// Return true iff pt1 is less than pt2.
return (pt1.second < pt2.second) or
((pt1.second == pt2.second) and (pt1.first < pt2.first));
}
Definespivot_less(links are to index).Used below.
And that's it. You can get some idea of the cost in complexity that better performance requires by comparing the test cases below to the test cases in the prior solution.
<chs-tri.cc>=
#include <algorithm>
#include <iostream>
#include "triangulations.h"
// Deja vu, c++ style.
static double dabs(double);
// What "close enough" means.
const double epsilon = 0.00001;
<an angle>
<the min-pivot functor>
<finding the smallest larger angle>
<inside points functor>
static inline double
dabs(double d) {
// Return the absolute value of the given value.
return d < -epsilon ? -d : d;
}
<minimal pivot less-than>
<pivot and rotate>
points
triangulations(const points & pts) {
points ans;
ans.c = pts.c;
const ptvec_iter
b = ans.c.begin(),
e = ans.c.end(),
g = tri(pts.g, b, e),
y = tri(pts.y, g, e);
ans.g.assign(b, g);
ans.y.assign(g, y);
ans.c.assign(y, e);
return ans;
}
#ifdef TESTING
// g++ -o tri-test -gstabs -ansi -pedantic -Wall -DTESTING new-tri.cc && ./tri-test
#include <cassert>
#include <cstdarg>
#include <set>
static ptvec
p2v(unsigned cnt, ...) {
ptvec pv;
va_list ap;
va_start(ap, cnt);
while (cnt-- > 0)
pv.push_back(point(va_arg(ap, int), va_arg(ap, int)));
va_end(ap);
return pv;
}
#define test_all(_pv, _t) \
std::sort(_pv.begin(), _pv.end()); \
while(std::next_permutation(_pv.begin(), _pv.end())) { _t; }
static void testt(
const point & p0, const point & p1, const point & p2) {
point pa[] = { p0, p1, p2 };
ptvec pv(pa, pa + 3);
test_all(pv,
assert(sweep(p0, angle(0, 0), pv) == p1);
assert(sweep(p1, angle(p0, p1), pv) == p2);
assert(sweep(p2, angle(p1, p2), pv) == p0);
)
}
static void same_pts(
const ptvec & pts, const ptvec_iter & b, const ptvec_iter & e) {
std::set<point>
ps1(pts.begin(), pts.end()),
ps2(b, e);
assert(ps1 == ps2);
}
static void includes_pts(
const ptvec & pts, const ptvec_iter & b, const ptvec_iter & e) {
std::set<point>
ps1(pts.begin(), pts.end()),
ps2(b, e);
ptvec pv;
std::set_intersection(ps1.begin(), ps1.end(),
ps2.begin(), ps2.end(),
std::back_inserter(pv));
std::set<point> ps3(pv.begin(), pv.end());
assert(ps3 == ps1);
}
int main() {
const point p00(0, 0), p04(0, 4), p40(4, 0), p11(1, 1);
ptvec pts;
point p0, p1, p2;
pts = p2v(3, 0, 0, 0, 1, 0, 4);
test_all(pts,
assert(sweep(p00, angle(0, 0), pts) == p04);
assert(sweep(p04, angle(p00, p04), pts) == p00);
)
pts = p2v(3, -1, 1, -5, 1, -2, 1);
p0 = point(-1, 1);
p1 = point(-5, 1);
p2 = point(-2, 1);
test_all(pts,
assert(sweep(p1, angle(0, 0), pts) == p0);
assert(sweep(p0, angle(p1, p0), pts) == p1);
)
testt(p00, p40, p11);
testt(p40, p04, p11);
ptvec grid;
for (int i = -5; i < 6; i++)
for (int j = -5; j < 6; j++)
grid.push_back(point(i, j));
pts = p2v(4, 0, 0, 1, 0, 1, 1, 0, 1);
same_pts(pts, grid.begin(), tri(pts, grid.begin(), grid.end()));
pts = p2v(4, 0, 0, 0, 1, 0, 2, 1, 1);
same_pts(pts, grid.begin(), tri(pts, grid.begin(), grid.end()));
pts = p2v(4, 0, 0, 0, 1, 0, 2, 1, 1, -1, 1);
same_pts(pts, grid.begin(), tri(pts, grid.begin(), grid.end()));
pts = p2v(4, 1, 1, 1, 2, 2, 2, 2, 3);
same_pts(pts, grid.begin(), tri(pts, grid.begin(), grid.end()));
pts = p2v(4, 0, -5, -3, 4, -4, -4, 1, 3);
includes_pts(pts, grid.begin(), tri(pts, grid.begin(), grid.end()));
pts = p2v(3, -4, -4, 2 -1, 4, 0);
includes_pts(pts, grid.begin(), tri(pts, grid.begin(), grid.end()));
pts = p2v(3, -1, 1, -5, 1, -2, 1);
assert(tri(pts, grid.begin(), grid.end()) == grid.begin());
pts = p2v(1, -1, 1);
assert(tri(pts, grid.begin(), grid.end()) == grid.begin());
}
#endif
Defineschs-tri.cc(links are to index).This code is written to a file (or else not used).
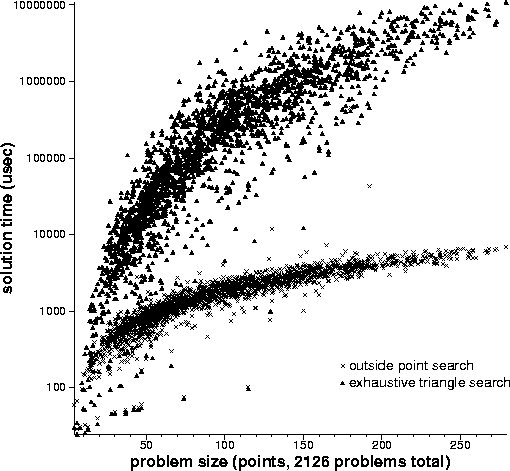
As a check, below is a graph of execution time vs. problem size for both solutions. As anticipated, the solution that searches for outside clear points is faster than the solution that exhaustively searches through all tirangles.
chs-tri.cc>: D1
es-tri.cc>: D1
This page last modified on 31 May 2003.