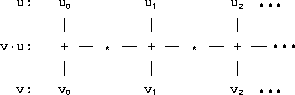
std::inner_product() generalized numeric algorithm computes
the inner product over two data sequence.
- That looks promising.
bool tableau::
operator == (const tableau & t) const {
if (pile_cnt() != t.pile_cnt())
return false;
piles_citer
i = piles.begin(),
j = t.piles.begin();
while (i != piles.end())
if (*i++ != *j++)
return false;
return true;
}
while i != piles.end()
if *i++ != *j++
return false
with a generic algorithm?
accumulate()
inner_product()
partial_sum()
adjacent_difference()
<numeric> header.
std::inner_product() algorithm works over two data
sequences.
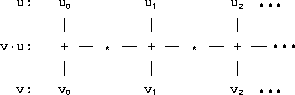
std::inner_product() generalized numeric algorithm computes
the inner product over two data sequence.
std::inner_product()std::inner_product() accepts two data sequences and returns
the inner product of the two sequences.
double ip =
std::inner_product(
v.begin(), v.end(),
u.begin(),
i);
i is the initial value of the inner product.
std::inner_product() is generalized because addition and
multiplication can be replaced by other binary operations.
== and logical and
&&.
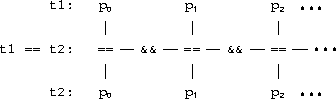
while i != piles.end()
if *i++ != *j++
return false
return true;
can be replaced with a redefined version of std::inner_product() to give
bool tableau::
operator == (const tableau & t) const {
return
(pile_cnt() == t.pile_cnt()) and
std::inner_product(
piles.begin(), piles.end(),
t.piles.begin(),
true,
std::logical_and<bool>(),
std::equal_to<pile>());
}
std::inner_product() always takes O(n) time.
std::equal() does the job with less fuss.
return
(pile_cnt() == t.pile_cnt()) and
std::equal(piles.begin(), piles.end(),
t.piles.begin())
std::equal() over std::inner_product().
std::inner_product() generalized numeric algorithm can operate
over two source data sequences.
This page last modified on 3 April 2003.