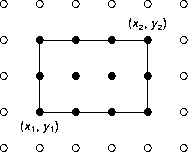This assignment is due by 2:00 p.m. on Tuesday, 19 March.
See the assignment turn-in page (last modified on 22 January 2002) for instructions on
turning in your assignment.
A rectangle with a diagonal having the endpoints (x1, y1) and
(x2, y2), all coordinates integers, can be thought of as the set
of points with integer coordinates that are either inside or on the boundary of
the rectangle; that is
rectangle = { (x, y) |
min(x1, x2) <= x <= max(x1, x2) and
min(y1, y2) <= y <= max(y1, y2) }
or, in pictures,
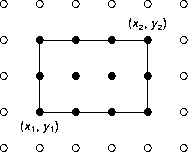
As defined, a rectangle always contains at least one point.
Once you start thinking about rectangles as sets of points, you can also start
thinking about performing set operations on rectangles. For example, the union
of two rectangles is the set of points that are in either rectangle; that is,
union R1 R2 = { (x, y) | (x, y) in R1
or (x, y) in R2 }
or, in pictures,
The intersection of two rectangles is the set of points that are in both
rectangle; that is,
intersection R1 R2 = { (x, y) | (x, y) in R1
and (x, y) in R2 }
or, in pictures,
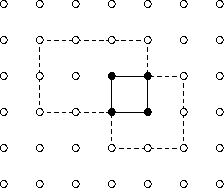
The difference of two rectangles is the set of points that are in the first
rectangle but not in the second rectangle; that is,
difference R1 R2 = { (x, y) | (x, y) in R1
and (x, y) not in R2 }
or, in pictures,
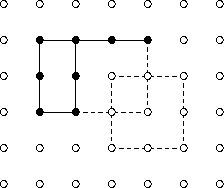
As the pictures show, applying a set operation to two rectangles usually
results in a set of points that is not a rectangle as defined here; the point
set may have notches or holes in it, or it may not have any points at all.
Never the less, to keep things simple, such point sets will be called
"rectangles" in what follows.
Write a program that manipulates rectangles as sets of integer-coordinate
points. The manipulations are controlled by commands read from std-in.
Commands come from std-in; each command fits on a line of text, and a line of
text contains at most one command; that is, lines containing no text are
acceptable input and should be ignored. The recognized commands are
- name
= rectangle x1 y1 x2 y2 -
Construct a rectangle with diagonal endpoints (x1, y1) and (x2,
y2) and assign the rectangle to name.
- name
= union name1 name2 - Form the union of
the rectangles assigned to name1 and name2 and assign the result to
name. Prints an appropriate error message to std-err if either of name1 or
name2 have not been assigned rectangles.
- name
= intersection name1 name2 - Form the intersection of
the rectangles assigned to name1 and name2 and assign the result to
name. Prints an appropriate error message to std-err if either of name1 or
name2 have not been assigned rectangles.
- name
= difference name1 name2 - Form the difference of
the rectangles assigned to name1 and name2 and assign the result to
name. Prints an appropriate error message to std-err if either of name1 or
name2 have not been assigned rectangles.
output [ name1 name2 ... ]-
Write to std-out a description of the rectangles associated with the given
names. If no names are given, describe all the defined rectangles. if any of
the given names have not been assigned rectangles
output should print an
appropriate error message to std-err and produce no other output.
Each piece of a command may be preceded and followed by space characters
(except for newlines); any space characters in excess of those needed to
separate one piece from the next should be ignored. An incorrectly formatted
or unrecognized input line should result in an informative error message to
std-err and the input line should be ignored. Errors should not end the
program.
All error output should be written to std-err. The only output that should
appear on std-out is the results of output commands.
Given a set of rectangles, the output command describes the contents of the
bounding box for the rectangle set. A bounding box for a set of points is
the smallest rectangle that encloses all the points
An output command produces output in the following form:
n
line 1
line 2
...
line n
where n is a non-negative number giving the number of lines being output;
n will be 0 if there is nothing to output.
Each line of output represents a horizontal row of points from the bounding
box; line 1 represents the first (topmost) row, line 2 represents the
second row, and so on.
Each row is described using run-length encoding, which represents a
sequence of n identical points (all rectangle points or all non-rectangle
points) by the number n. The points in a row are described in
left-to-right order, and the first number always describes the number of
rectangle points; if the left-most points in a row aren't rectangle points,
then the first number is 0. The numbers in each row should should sum to the
same value.
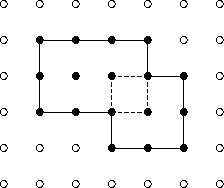
For example, in the rectangle set
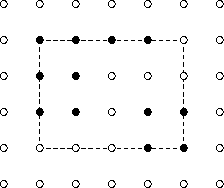
the rectangle points solid and the non-rectangle points are outlined; the
bounding box is outlined with dashes. Given this rectangle set, output
would write the following to std-out
4
4 1
2 3
2 1 2
0 3 2
The program show-output in /export/home/class/cs-509/pa4 displays images
based on the data produced by output commands. One way to use show-output
is to pipe the output of your rectangle program into it:
rectangles | /export/home/class/cs-509/pa4/show-output
assuming your program is called rectangles. Your program still takes
input from the keyboard, but the output goes to show-output (you may have
to move the mouse out of and back into your terminal window if your window
manager shifts the focus to the show-output display window).
If you want to see the output passing between your program and
show-output, stick a tee between them:
rectangles | tee /dev/tty | /export/home/class/cs-509/pa4/show-output
This command copies the output going to show-output and writes it to your
terminal window. If you replace /dev/tty with the name of a file,
tee will write the output to the file and not your terminal window. See
the tee man page for more details.
You must be sitting in front of a machine that's running the X Window System to
be able to see the images displayed by show-output. If you're sitting in
front of a Sun, a Silicon Graphics machine or a PC running Linux and you're
also running a window system, then you can use show-output. If you're not
running a window system, or if you're sitting in front of a PC running any
Microsoft product, then you can't use show-output.
This page last modified on 10 March 2002.