Advanced Programming II, Spring 2002

Programming Assignment 2 - An Example Solution

Table of Contents

Introduction

This page gives a solution to the second programming assignment, which involved writing a simple constant-value optimizer for statement blocks.

Design

Reading the problem statement a couple of times fairly well establishes the overall purpose of the program: repeatedly read a statement block, optimize the statement block, then write the statement block.

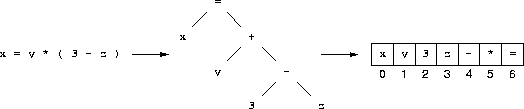
Assuming we understand what a statement block is, this translates directly into a main() routine: 

<main()>= (U->)

int main() {

  statement_block sblock;
  std::string sep;

  // All statement blocks of interest are either still in std-in or have
  // been read from std-in, optimized, and written to std-out.

  while (sblock.input(std::cin)) {
    sblock.optimize();

    std::cout << sep;
    sblock.output(std::cout);
    sep = "\n";
    }

  // All statement blocks of interest are either still in std-in or have
  // been read from std-in, optimized, and written to std-out, and std-in is
  // empty. 

  }
Defines main (links are to index).

Almost by inspection this code is correct, assuming statement blocks are implemented correctly. But what are statement blocks? Reading the problem a few more times gives us some hints, and main() supplies the rest.

The problem tells us that a statement block is a sequence of one or more statements, and that statements are never deleted from a statement block (this last bit comes from understanding the optimizations). These facts suggest that a vector of statements might be a good representation for a statement block, assuming we know what a statement is.

The problem suggests what statement blocks might be; main() tells us what statement blocks must do: input, optimize, and output. Together, we have enough information to develop a first-cut at defining a statement block:

We now have two sub-problems to solve: figuring out how statement-block operations are implemented, and figuring out what a statement is. Because statements are probably going to figure in how statement-block operations are implemented, it's a good idea to assume we know what statements are, and use them to implement the statement-block operations.

Unfortunately, while main() tells us what the statement-block operations are, it doesn't tell us how they're implemented. Again, however, the problem statement tells us (perhaps indirectly) what we need to know. A statement block is a sequence of statements delimited by blank lines; ergo, to input a statement block we need to input the statements between blank lines and store them in a block:

main() requires that input() return false when it has no more blocks to read. Also note that we assume that a statement can be created from a string containing a textual-representation of a statement.

Outputting statement blocks is even easier than inputing it, because we don't have to go searching around std-in to find them.

Optimizing statement blocks first appears as if it could be implemented in the same way as outputting them: let each statement optimize itself. This approach is almost correct, but overlooks an important point about constant folding: to correctly constant fold a statement, the optimization needs to know which variables have been equated to constants. The statement block is the proper place to manage this information, because individual statements don't have the overall scope required.

With these refinements, the design of the statement block optimizer is 

optimize()
  mapping m

  for i = 0 to block.size()
    block[i].optimize(m)

where mapping is some data structure that maintains the variable-constant correspondence.

That takes care of the design of statement blocks. We still have to design statements, and we've introduced a mapping as a new data structure. A mapping appears to be a simple dictionary-like data structure with the variable as the key and the constant as the entry, so we won't consider it further in the design.

Turning to statements, we finally have to do some serious design work. The statement block design set the statement's public interface, but left open the choice of internal representation. Using a string to represent a statement is one possibility, but a little thought shows it's not a good possibility for at least two reasons:

  1. it's difficult to manipulate a string in the way that the optimizations require,

  2. and strings ignore almost all the structure present in statements, which makes them harder to analyze.

If a string is too hard to deal with, how about breaking it up into a sequence of substrings, where each substring is a piece of the original statement? This makes it easier to manipulate the statement - substituting a constant for a variable, for example - and makes some analyses easier - making sure values appear on either side of an operator, for example.

A sequence of substrings is an improvement over a single string, but it still doesn't exploit all the structure in a statement. In particular, it's difficult to analyze a sequence to determine operator order as determined by precedence and associativity. One possibility is to exploit the fact that a statement is made up of binary operators and represent the statement as a binary tree (treating assignment as an operator for the moment). Not only does this make the operation ordering obvious, but it gets rid of the parentheses, and is a handy form for optimizing.

The only problem with binary trees is we have to do a lot of work to implement them; we have define the node class and use difficult and dangerous dynamic memory programming to create the trees. It would be great if we could have trees in a form supported by the STL. And fortunately, we can walk the tree to linearize it and store the nodes in a vector. An inorder walk brings us back to a sequence of substrings; a pre-order walk puts the working end of the tree at the wrong end of the vector (the root would be at element 0), leaving a post-order walk to create a postfix representation.

To summarize, we are thinking about going from a string to a tree to a postfix stack:

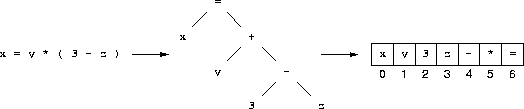
a statement transformation

But, the transformation still requires that we build a binary tree, which is what we were trying to avoid in the first place. Is there some way to go directly from the string to the postfix stack without a binary tree? A trip back to the problem statement gives us the answer we need. After re-reading the description of an expression and fiddling around a bit with a paper and pencil, it should be clear that a statement has the following form:

value1 op1 value2 op2 value3 . . . valuen opn valuen + 1

where n is at least 1 and value is either a variable, a constant or an expression between parentheses (in fact, value1 is a variable, and op1 is an assignment operator, but we'll ignore this for a moment).

Now we're almost there. Because all operators are left-associative, a right to left scan of statement is enough to generate a postfix representation for the statement: get the right operand valuei + 1 and operator opi, then recursively translate the left operand to postfix. Pushing the left, then right operand followed by the operator completes the transformation. If one of the values is a parenthesized expression, then recursively translate the expression inside the parentheses to postfix.

The last bit we have to clean up is value1 and op1, the variable and assignment statement. The problem here is assignment is right associative, not left associative. However, that's easily dealt with by stopping the transformation when it reaches the assignment operator and inserting it "by hand" on the top of the stack; this puts the assignment in proper postfix order, and the whole statement has been translated.

Before going on, it would be wise to make sure that optimization and output can work with a statement represented in postfix form. Output is equivalent to converting the postfix stack into a string, which is easily done with a recursive procedure: 

postfix2string(stk)
  opr = stk.pop
  right = postfix2string(stk)
  if is_expression(right)
    right = "( " + right + " )"
  left = postfix2string(stk)
  return left + " " + opr + " " +right

There is one subtlety with this code: if the right operand is an expression, it must be placed in parentheses to make sure the whole expression is evaluated before the operation takes place.

Optimization has a similar recursive structure: recursively optimize the left and right operands, then optimize the expression itself. 

optimize(stk)
  opr = stk.pop
  right = optimize(stk)
  left = optimize(stk)
  if left and right are constant
    optimize
  else
    push back left, right, and opr

That more or less concludes the design of an statement block optimizer. The one main issue left is dealing with errors. There are two techniques for dealing with errors: freaking out or pretending that nothing's wrong. Freaking out corresponds to throwing an exception, while pretending nothing's wrong corresponds to defining a special error statement. The disadvantage to using a special error statement is the code becomes cluttered with checks for errors (an error statement doesn't get optimized, for example); the disadvantage to using exceptions is providing correct resource management in the face of arbitrary termination. Because ugly code is marginally better than broken code, we'll assume a special statement to handle errors.

There are many other, smaller details to be worked out, but now that we have the general outline of the program designed, we'll have enough guidance to handle them as they come up during implementation.

Implementation

Statement Blocks

Most of the statement-block code is simple enough to be described directly in the design section. Statement-block optimization had a bit of complexity to it, and the design only sketched out an implementation.

Statement-block optimization proceeds statement-by-statement, with each statement doing its own optimization. If an error occurs during optimization, the whole block is replaced with the error statement.

Statements

The externally visible parts of the statement class are given by the statement block class: create a statement from a string, optimize a statement under a particular set of variable assignments, and output a statement to a stream.

Within the class, a statement is represented in postfix form in the word stack stmt. Linearly, the stack top appears to the right; if s is x = y + 1, stmt ends up being x y 1 + = with = at the top of the stack and x at the bottom.

Inside the class, things are a bit messier. The constructor statement() uses a couple of helper routines to check for syntax errors and to translate s from infix to postfix. statement::optimze() uses a couple of helper routines to optimize a statement. And even statement::output() uses a helper routine to produce the string to output. statement() constructs a statement instance based on the statement given in s; the word stack stmt contains the postfix version of s. stmt is initialized to contain s in infix order; the body of the statement() turns the order into postfix. The statement in s is not optimized here; it is just checked for syntax errors and turned from infix to postfix form.

If a syntax error is discovered during the translation of s, stmt contains a single error word describing the problem.

Try to optimize the binary expression l o r; if the expression can be optimized, place the result in opt and return true; otherwise return false. Both operands are constants; evaluate the constant expression and store there result in opt. The argument-value checking is minimal, but the idea should be clear. Even if both operands aren't integer values, it may still be possible to optimize the binary expression using some arithmetic properties, such as x + 0 = 0 + x = x. To optimize a statement, pop the assignment operator and optimize the expression on the right-hand side. After the expression has been optimized, stmt should contain the assignment's left-hand side. If the statement is an error statement; don't do anything. Return true if and only if optimization went o.k.; return false on an error. Optimize the postfix expression given at the top of expr in the context of the mapping m; return the optimized postfix expression in a word stack.

If the expression is a constant, return the constant. If the expression is a variable and the variable has an associated integer, return the integer (that is, fold the constant); otherwise, return the variable. If the expression is a binary expression, optimize the expression's two operands, and then optimize the expression itself, if possible (that is, try to compile-time evaluate constant expressions). Return the optimized result if it exists, otherwise return the binary expression (in postfix form).

Printing a statement is most easily done by breaking it up into two parts: creating the string the print and then printing the string. statement::output() prints the string. Translate the postfix expression given in the word stack stmt into an infix expression represented as a string; the expression translated is popped off stmt.

Variables, constants and errors are returned as themselves. Given a binary expression (and at this point we can consider assignment to be another binary operation), convert the two operands into infix strings and catenate them with the operator to form the infix string.

The return value is true if and only if the returned string is an expression with binary operators. The return value is used to determine if right operands need be surrounded by parentheses to preserve evaluation order. For example, without parentheses the right expression in a + ( b + c ) would be a + b + c which, because of left associativity, is not the order of evaluation specified by the original expression. When the right operand to a binary expression is another binary expression, the right operand needs to be surrounded by parentheses to make sure it is evaluated properly.

Parse the expression at the top of the unparsed word stack and return it in postfix form. Expressions are parsed from right-to-left from the word stack unparsed; the right-most part of an expression must be a value. The right value may be preceded by an operator (as in left + right), an open parens (as in ( right )) or by the assignment operator (as in x = 1. In the last two cases, the expression is complete and the right value is returned as the expression (the open parens or assignment operator is left on the stack to be dealt with by the caller of parse_expr()).

If the right operand is followed by an operator, then the left operand is an expression because the operators are all left-associative. If the left operand can be successfully parsed, the expression found at the top of unparsed is returned in a new word stack in postfix form: the left expression followed by the right value followed by the operator (as in left right +.

Parse the value at the top of the word stack unparsed and return it in postfix form. A value is either a constant, a variable, or an expression in parentheses. The parsed value is returned in a word stack because an expression may contain more than one word. * 
<statement.h>=

#ifndef _statement_h_defined_
#define _statement_h_defined_

#include <fstream>
#include <string>
#include "mapping.h"
#include "word-stk.h"

<the statement class definition>

#endif


<statement.cc>=

#include "statement.h"
#include "str-utils.h"
#include <cstdlib>

using std::string;

<internal statement procedure definitions>

<statement procedure definitions>
Defines statement.cc, statement.h (links are to index).

Words

The components of a statement - variables, constants and the rest - need to have a representation, which will be called a word. The rest of the code doesn't demand much of words; a word needs to indicate what it looks like in text - its print representation or prep - and it needs to indicate what type of word it is. The primary word constructor accepts a word's print representation and uses it to set the word's type. This constructor can return a word of any type; any print representation that doesn't match any legal category is considered to be an error. It will be convenient to have a constructor that returns an constant word given an integer value. A predicate to test a word's type.

The Word Stack

Like the name suggests: a stack of words. Constructors can build an empty word stack, a word stack containing a single, given word, and a word stack derived from a string containing a statement; in the last case, the rightmost word in the statement appears at the top of the stack. It's a stack, so it needs stackish operations. pop() returns the word popped, unlike the STL pop routines. In addition to pushing a single word on a stack, push() can push one word stack on another, so that the top of the given stack becomes the top of the pushed stack; the given stack is unchanged. Should an error be found in the statement being held in a word stack, the stack is changed to an error stack, which contains a single error word having the given error message as its print representation. size() returns the number of words in the stack; is_error() returns true if the stack contains only the error word. The word stack constructors. 
<word_stk procedure definitions>= (U->) [D->]

word_stk::
word_stk(void) { 
  }

word_stk::
word_stk(const word & w) { 
  wdq.push_back(w);
  }

word_stk::
word_stk(const string & s) { 

  std::vector<string> pieces = split(s);

  for (unsigned i = 0; i < pieces.size(); i++) {
    word w = word(pieces[i]);
    if (w.type == word::error_word) {
      wdq.clear();
      w.prep = string("Unexpected word \"") + w.prep + "\"";
      wdq.push_back(w);
      return;
      }
    else
      wdq.push_back(w);
    }
  }
Defines word_stk (links are to index).

The stack operations. These would be much easier to implement if we know about the STL stack adaptors, but because we don't, we'll do it the hard way (or the more educational way) using vectors.

Turn the word stack into an error word stack. This code is a bit dodgy because it assumes word() will interpret emsg as an error message. It always will for this program, but in general this is bad programming because the code should insure an error word gets created, rather than relying on the good behavior of the callers to error(). Word stack query functions.

Mappings

The optimizer uses a mapping to keep track of which variables are assigned constant values.

A mapping supports four operations:

  1. Associate an integer with a variable.

  2. Determine if a variable has an associated integer.

  3. Return the integer associated with a variable.

  4. Remove an variable-integer association.

All these operations can be performed by an STL map, but because we haven't talked about maps yet, we'll do it the hard way and make our own data structure.

An association is just a pair of words; and a mapping is a vector of associations. Add the (var, val) association to the mapping; if var already is associated with an integer, val replaces the previous value. Return true if and only if var is associated with an integer in the mapping. Return the integer associated with var in the mapping; die if var doesn't have an association. Drop the association involving var from the mapping; die if var doesn't have an association. This will be much easier to implement once we learn about iterators. Return the mapping index for the association involving var or -1 if there's no such association.

main()

<main.cc>=

#include <iostream>
#include <string>
#include "statement-block.h"

<main()>
Defines main, main.cc (links are to index).

String Utilities

A convenient definition of the string-index type. Return true if and only if the given string is blank; that is, contains only space characters. Empty lines are considered blank. What space characters are. Split the given string into pieces at the given delimiter set (default is the space characters); only the non-empty pieces are returned. Return true if and only if the given string contains a possibly signed integer. Read the next non-blank line from the given input stream into the given string; return true if and only if the given string has a non-blank line.

Index

This page last modified on 26 February 2002.