Programming Assignment 5
Sliding Rectangles

Table of Contents

• Due Date
• Problem
• Input
• Output
• Program Behavior

This assignment is due on Tuesday, 27 March, no later than 2:00 p.m.

See the assignment turn-in page for instructions on turning in your assignment.

Piles of rectangles on a plane is an important geometric model for many algorithms; anybody who's used a windowing GUI is familiar with the model, as is anybody who's worked with VLSI design and analysis algorithms.

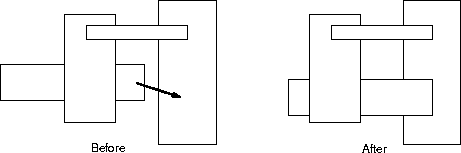
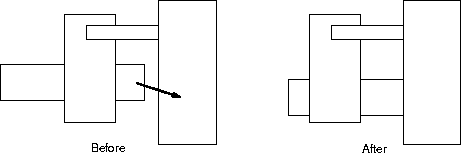
You'll be implementing an algorithm and program for manipulating rectangles by sliding them around on a plane. Although rectangles are two-dimensional figures, it will be helpful to think of them as being three dimensional, having a slight thickness as if they were made from paper.

A rectangle is defined by the end-point coordinates of one of its diagonals.

Either diagonal may be given.

A rectangle x₁ y₁ x x₂ y₂ encompasses the point (x_p y_p) if

min(x1, x2) < xp < max(x1, x2)

and

min(y1, y2) < yp < max(y1, y2)

Notice that a point on the edge of a rectangle is not encompassed by the rectangle.

Two rectangles overlap if there exists at least one point (including a point on the edge) of one of the rectangles that is encompassed by the other rectangle. Notice that two rectangles sharing only a common edge don't overlap.

If two rectangles overlap, one of the rectangles is above the other; the rectangle that is not above is below. For example

rectangle 1 is below rectangle 2; rectangle 2 is above rectangle 1.

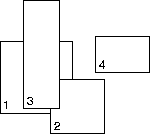
Every rectangle has a level, which is a finite, non-negative integer defined as

1. A rectangle that is not above any other rectangle has level 0.

2. A rectangle R that is above one or more rectangles has level L + 1, where L is the largest level of any rectangle below R.

For example, in the previous figure, rectangle 1 has level 0, and rectangle 2 has level 1.

Your program reads input from std-in. Input appears in one of two forms. Input of the form

x1 y1 x x2 y2

is interpreted to mean "construct a rectangle with diagonal at (x₁ y₁), (x₂ y₂)". The new rectangle lies above any rectangles it overlaps.

Input of the form

x1 y1 -> x2 y2

is interpreted to mean "slide the topmost rectangle encompassing the point (x₁ y₁) x₂ units to the right and y₂ units up" (where either x₂ or y₂ may be negative, in which chase movement is to the left or down, respectively). If no rectangle encompasses x₁ y₁, then nothing happens.

There are two rules your program must obey when sliding rectangles:

1. When a sliding rectangle begins to overlap a rectangle it hasn't overlapped before, the sliding rectangle is above the stationary rectangle.

   

2. If, by overlapping on top of a stationary rectangle, the sliding rectangle forms a cycle of overlapping rectangles, then the sliding rectangle is below the stationary rectangle.

   

At end-of-file from std-in, your program should output the rectangles from level 0 to the top level, one rectangle per line, using the same format in which they were read. Rectangles at the same level may be printed in any order.

For example, if the configuration of rectangles at end-of-file is

your program should produce either of the outputs

	or
x11 y11 x x12 y12			x41 y41 x x42 y42
x41 y41 x x42 y42			x11 y11 x x12 y12
x21 y21 x x22 y22			x21 y21 x x22 y22
x31 y31 x x32 y32			x31 y31 x x32 y32

Because rectangles 1 and 4 are both have level 0, they may be output in either order, but both must be output before rectangles 2 and 3.

Your program must work sensibly for all possible inputs. If the input is correct, your program must perform the operation correctly; if the input is incorrect, your program should print an error message and stop with no further actions.

This page last modified on 13 March 2001.