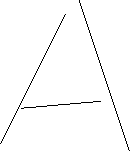A handwriting recognition program accepts as input a sequence of pen strokes
representing characters (letters and digits, for example) and produces as
output a sequence of characters corresponding to the input pen stokes.
Because of the variability of human handwriting, even when only one person is
doing the writing, a handwriting recognition program has to consider several
possible interpretations for input strokes. For example, the pen stoke
sequence
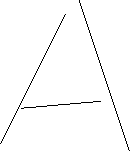
could be interpreted as the
character A or the character H. In this case, the intended character is clear,
but in the more general case the choice may not be so obvious. The output of a
handwriting recognition program represents the program's best guesses as to the
intended characters; in cases where there is no clear-cut interpretation, the
program may include several of its best guesses in its output.
Handwriting recognition programs generally work in two phases: a training phase
and a recognition phase. In the training phase, the program inputs a sequence
of pen strokes representing several carefully drawn versions of the same
character. The program processes these training strokes to learn the general
features of the character being input.
Once the program has been trained on all the characters it needs to recognize,
it moves to the recognition phase. In the recognition phase, the program reads
a sequence of strokes, extracts the features of the strokes, and tries to match
the features against the set of training features. Based on the number and
strength of the matches, the program then outputs its best guess (or guesses)
as to the character represented by the input strokes.
The program /export/opt/cs-509/pa4/gen-chars generates the strokes for a handwritten character.
The command line format is
gen-chars [-w n] c. . .
where n is a number, 0 <= n <= 100, and c one of the letters A
through Z (in either case). The -w option is the wildness parameter,
which indicates how far from the training data the handwritten strokes may
deviate. A 0 wildness parameter indicates no potential deviance from the
training strokes; a 100 wildness parameter indicates maximum potential deviance
from the training strokes (remember that the strokes are probabilistically
distorted: it is possible, although unlikely, that the strokes produced with a
100 wildness parameter may match exactly the training-set strokes).
The stroke sets output by gen-chars have the same format as they do in the
as the training file: a sequence of strokes, one per line, with a sequence of
coordinate pairs for each stroke. Stoke sets are separated from each other by
a single blank line; there are as many stoke sets as there are characters given
on the command line; and the stroke sets appear in the same order as the
left-to-right order of the characters on the command line.
gen-chars distorts the strokes in three ways:
- It adds a random jitter xj and yj to the x and
y coordinates of each point along the stroke; this has the effect of
making each stroke more or less shakey, depending on the size of the jitter
added. The values of xj and yj may vary for each coordinate.
- It adds a constant xt and yt translation to each
coordinate; this has the effect of moving the character around the page, and
simulates the fact that a character can appear anywhere on the surface of the
input device. Unlike the jitter values, the translation values xt and
yt are constant for all coordinates in a particular character; they may,
however, vary from character to character.
- It multiplies each coordinate by a constant scale s; this has the
effect of changing the overall size of the character. The scale value s
is constant for all coordinates in a particular character, but may vary from
character to character.
These are the only distortions gen-chars applies to the strokes.
Your program should read the training-set data, construct whatever data
structures it needs, and then read character stroke sets from std-in. A stroke
set has the same format as the training-set data, but without the character
identifier: a sequence of strokes, with each stroke being a sequence of at
least two points, with each point being an x y pair. Successive
stroke sets are separated by one blank line (This format is the same as the
output produced by gen-chars).
Your program should print to std-out its best guess as to the characters
represented by input stroke sets. The characters should be output one per
line, in the same order as the stroke sets. If your program can't decide the
best character represented by a particular stroke set, it should print out the
candidates in order of decreasing probability on the same line.
For example, if your program read three stroke sets and produced the output
A
R K P
Z
then your program definitely recognized the first stroke set as representing an
A; recognized the second stroke set as most likely representing an R, but
also possibly representing a K, and less likely representing a P; and
definitely recognized the third stroke set as representing a Z.