1. Let A be an array of integers that has been turned into a heap. Can A be interpreted as a topological sort? Explain your answer.

   ---

   No. In a topological sort, if item X is less than item Y, then X should appear before Y in the topological sort. In a heap, if a parent is less than its children, then the parent should appear before the children in the heap, but the children may appear in the heap in any order. For example, 1, 2, 4, 16, 5 is a valid heap but an invalid topological sort.

   ---

2. The following binomial trees are pieces of the same binomial heap:

   

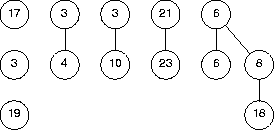
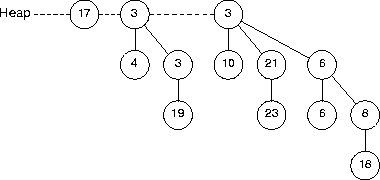
   Using all and only the pieces shown here, reconstruct the binomial heap.

   ---

   Because there are 13 nodes in the binomial heap, we can expect the heap to contain a B₀, a B₂, and a B₃ binomial tree. As long as each tree obeys the heap property, it doesn't make any difference which pieces go into each tree. One possible heap is

   

   ---

3. A colleague of yours has invented a new form of open-address hashing called move to the start hashing. When searching for item x, move to the start hashing remembers i = h(x, 0). If x is found at table element j, then swap T[i] and T[j]. Your colleague would like to know your opinion of move-to-the-start hashing; what do you say? Be sure to explain your answer.

   ---

   If your colleague is using linear probing, move to the start hashing is a good idea (or, at least, not a bad idea). Assuming h(x, 0) is a miss, then x will be found lower down in the table; moving x up to T[h(x, 0)] means x will be found earlier. As for the element originally in T[h(x, 0)], either it hashes directly to that slot or was placed there because of collisions higher up in the table; in either case, moving the element further down the table means it will still be found, although it will take a few more probes to do so.

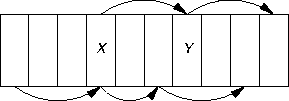
   If your colleague is using a quadratic or double hash function, then move to the start hashing is a bad idea. The problem is two entities may collide, but be on different probe sequences; switching the entities may move one of them out of range of its probe sequence. For example, consider the hash table

   

   Suppose X was placed using the lower probe sequence and Y was placed using the upper probe sequence. If Y is swapped with X, then X gets moved out of its probe sequence, and effectively gets lost.

   ---

4. A colleague of yours is writing a compiler and wants to have it keep track of the following information:

   1. The character constants used in the program being compiled.

   2. The language's keywords.

   3. The identifiers used in the program being compiled.

   Your colleague comes to you for advice about which kind of hash table would be most appropriate for each kind of information. What do you recommend? Don't forget to explain to your colleague why your choice is the most appropriate among all possible choices.

   ---

   Character constants are small values, typically seven or eight unsigned bits, so a direct-addressed hash table would be most appropriate here; in fact, a direct-addressed bit map would be best.

   A programming language has a fixed number of keywords known in advance, so the arbitrary storage capacity of a closed-address hash table isn't needed here. Keywords are generally multi-character strings, and are too big to directly interpreted as index values, meaning direct-address hash tables wouldn't work too well, leaving open-address hash tables.

   There can be an arbitrary number of different identifiers used in a program, which means that there's always a danger of overflowing an open-addressed hash table. Single-character identifiers are frequent, but so are long, multi-character identifiers, so direct-addressed hash tables aren't appropriate, leaving closed-address hash tables as being most appropriate for storing identifiers.

   ---

This page last modified on 15 March 2000.