1. Turning an undirected graph into a directed graph involves replacing each undirected graph edge (u, v) with the two directed edges (u, v) and (v, u). Explain which graph representation is better suited for this operation.

   ---

   The two graph representations are adjacency list and adjacency matrix. Starting from an undirected graph, both are equally well suited; see Figure 23.1 in the text.

   ---

2. The Bellman-Ford algorithm normally relaxes each edge |V| - 1 times to produce a shortest-path tree. Under which conditions would Bellman-Ford produce a shortest-path tree after relaxing each edge once?

   ---

   The one fact we know about advancing the shortest path by one step is that if v_{n - 1} is the next-to-last vertex on the shortest path from s to v_n, then d[v_n] = d[v_{n - 1}] + w(v_{n - 1}, v_n).

   If Bellman-Ford relaxes all vertices on the shortest paths from s in breadth-first order from the start vertex, it will find the single-source, all destinations shortest paths in one pass.

   Bellman-Ford doesn't, in general, know that the shortest paths through a graph are before it starts. However, if the graph is a tree, then the shortest paths are clear, and Bellman-Ford will find them in one pass if it relaxes the edges in breadth-first order.

   ---

3. Explain the basic idea behind modifying Dijkstra's algorithm so it could handle graphs with at most one negative edge. Do not modify the algorithm; just explain the idea you'd follow to do so.

   ---

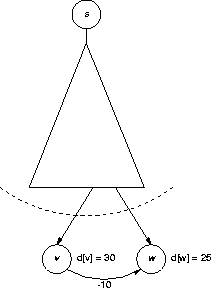
   Dijkstra's algorithm fails on graphs with negative weights because negative weights invalidate the assumption that the shortest path to the vertex v with the lowest distance on the other side of the frontier follows the edge connecting v to the shortest-path tree. For example, consider this snapshot in an execution of Dijkstra's algorithm:

   

   The triangle is the shortest paths found so far and the dotted line is frontier. Dijkstra's algorithm adds w to the shortest-path tree because d[w] = 25 < d[v] = 30. However, the shortest path to w actually goes through v along the negative-weight edge, giving d[w] = 20.

   Dijkstra's algorithm can be adjusted to handle a single negative edge by changing the test for the smallest distance vertex across the frontier. The new test will check to see if the smallest distance vertex is smaller than the next larger distance vertex by at least absolute value of the negative weight. If it is, then the smallest distance vertex truly is the smallest distance because any other path, even if it includes the negative-weight edge, will not be smaller.

   This fix doesn't work in all cases; for example in the snapshot above, d[v] - d[w] = 5 < |-10|, and the modified Dijkstra's algorithm would have to give up.

   ---

4. Why does Prim's algorithm correctly handle graphs with negative edges?

   ---

   Prim's algorithm works because it has complete information: one of the edges crossing the cut must be part of the spanning tree. Dijkstra's algorithm works with partial information: it knows of one path to the vertices across the frontier, but there may be other paths it doesn't know about, which requires the assumption that the other paths are no shorter than the known path.

   ---

This page last modified on 12 February 2000.