For example, suppose a three-inch sub has calorie counts (100, 150, 120) and k = 2. Leaving the sub undivided results in one piece with calorie count 100 + 150 + 120 = 370. The sub can be divided into two pieces in two ways: (1 inch, 2 inches) and (2 inches, 1 inch). In the first case, the calorie counts are (100, 150 + 120 = 270); in the second case the calorie counts are (100 + 150 = 250, 120). Because the maximum-calorie piece in the second case (250) is smaller than the maximum-calorie piece in the first case (270) and in the undivided case (370), it is the way the sub should be divided.
As you might expect, dividing up the sub gets more complicated as n and k get larger. Recognizing your expertise as an algorithm designer, the Weight Watchers club asks you for an algorithm to divide the sub according to the rules given above. Also, because the sub usually arrives a few minutes before the meeting starts, they ask that your algorithm be tractable.
A number of people tried to solve this by first arranging the inches of the sub in increasing (or decreasing) order by calorie count, in preparation for a greedy solution. Unfortunately, the problem says you can only cut the sub, not re-arrange it. A few other people tried to draw an analogy between this problem and the matrix multiplication problem. Nobody could convincingly describe in what way the two problems are analogous, and I find the analog murky (to start, the matrix chain had to be fully parenthesized, but the sub had to be cut into no more than k pieces).
Divide the sub as required. Assume the cuts were made from left to right and consider the leftmost (that is, first) cut. Because the maximum piece should be as small as possible, the sub to the right of the cut should be divided to minimize the maximum piece; that is, the division of the sub to the right of the first cut is optimum too. The one piece to the left of the first cut is optimum, so the optimum subproblem holds.
The previous paragraph leads naturally to a recursive solution:
int divide-sub(n, k)
m <- infinity
for i <- 1 to n
m = min(m, max(divide-sub(i, k - 1, sum(j = i + 1 to n, c(i))))
return m
divide-sub() does exponential work, but there are only polynomially many
subproblems, which you can tell by counting the parameter values to
divide-sub(). The repeated subproblem property holds, and there should be
a dynamic programming solution to this problem.
Let M be an n by k matrix if integers. M[i, j] contains the size of the largest sum of the last i inches of the sub when divided into at most j pieces. The initial conditions are M[1, for 1 <= j <= k and M[n = sum(i = 1 to n, si). Assuming M has been initialized, the algorithm is
divide-sub(c, n, k)
for i <- 2 to n
for j <- 2 to k
M[i, j] <- infinity
for k <- 1 to i - 1
s = max(M[k, j - 1], sum(l = x to i, c(l)))
if M[i, j] > s
M[i, j] = s
Many people drew the analogy between this problem and the 0-1 knapsack problem. At first I thought the analogy was not particularly useful but otherwise harmless. However, it turned out many people focused on the wrong part of the analogy: in the 0-1 knapsack problem, item k is either in the knapsack or it isn't (that's why the knapsack is 0-1). In this problem, however, as many slices as possible from ingredient i can be included in the sub. A direct application of the 0-1 knapsack solution to this problem will fail because you need to keep track of how many slices of i are in the sub, not just whether or not there are slices of i.
First, note that instances of this problem may not have a solution; for example, slices with an even number of calories can't make a sub with an odd number of calories. On the other hand, if one of the slices has one calorie, a solution always exists for any sub.
We can use either greed or dynamic programming to derive an approximation algorithm for this problem. Greedy algorithms are usually simpler and faster to develop (and run) than are dynamic programming algorithms, so let's go with that.
Assume there are n ingredients available for making subs, and let the
array cal store the calories per slice in descending order so that
ingredient i has cal[i] calories per slice. The greedy algorithm
makesub() returns the number of slices of each ingredient required to make
a sub of no more than C calories:
[int] makesub(C)
i <- 0
slices <- [0, ..., 0]
while (i < n) and (C > 0)
if C > cal[i]
C <- C - cal[i]
slices[i]++
return slices
makesub() find an optimal answer when one exists? Unfortunately, it
does not. Suppose C = 35 and cal = [31, 20, 15, 1]. The optimal
solution is slices = [0, 1, 1, 0], but makesub() returns [1, 0, 0,
4]. This problem does not exhibit the greedy choice property.
Unfortunately, the program that determines the conveyer-belt part sequence occasionally produces an sequence that's incorrect (for example, p1, q2, p2, q1, ...). Acme would like you to write a program that accepts as input the conveyer belt sequence c1, c2, ..., cm + n and the two part sequences p1, ..., pn and q1, ..., qm and determine if the conveyer-belt sequence is a proper interleaving of the part sequences. Acme would like your algorithm to be as efficient as possible.
To restate the problem more compactly: Given the three string S, S1 and S with |S| = |S1| + |S2|, do S1 and S2 interleave to produce S?
First, let's take a look at what doesn't work: a linear scan through S. Linear scan may incorrectly fail when S1 and S2 have common parts. For example, consider
A linear scan through S to find S1 latches onto the first b in S; removing S1 turns S into acb, which is not equal to S2 and the linear scan concludes that S is not an interleaving of S1 and S2. However, that S = S2S1.
S = abcb S1 = b S2 = abc
This problem has a simple brute-force solution: generate all possible interleavings of S1 and S2 and check to see if each interleaving equals S. Form an n-bit vector where n = |S| and bit i corresponds to the ith character in S. When i is 1, assume the corresponding character in S came from S1, otherwise the character came from S2. Generate all possible n-bit vectors, extracting each interleaving from S and checking it against S1 and S2. This is an exponential algorithm.
How does this problem subdivide? If S is an interleaving of S1 and S2 then either S[0] = S1[0] or S[0] = S2[0]. If, for example, S[0] = S1[0], then S[2 ..] is a interleaving of S1[2 ..] and S2; that is, the optimal subproblem property holds. The recursive algorithm follows directly:
bool interleaving(S, S1, S2)
if |S1| + |S2| = 0
return |S| = 0
if S[0] = S1[0] and interleaving(S[2 ..], S1[2 ..]), S2)
return true
return S[0] = S2[0] and interleaving(S[2 ..], S1, S2[2 ..])
We can exploit the repeated subproblem property with a boolean matrix M of dimension |S1|x|S2|. The matrix element M[i, j] is true if and only if the substring S[0 .. i+j-1] is an interleaving of the strings S1[0 .. i-1] and S2[0 .. j-1]. M[i, j] is true if and only if
- M[i-1, j] is true and S[i + j - 1] = S1[i] or
- M[i, j-1] is true and S[i + j - 1] = S2[j]
The dynamic programming version follows immediately
bool interleaving(S, S1, S2)
M[0, 0] <- true
for i <- 1 to |S1| - 1
M[i, 0] = M[i - 1, 0] and S[i - 1] = S1[i - 1]
for i <- 1 to |S2| - 1
M[0, j] = M[0, j - 1] and S[i - 1] = S1[i - 1]
for i <- 1 to |S1| - 1
for j <- 1 to |S2| - 1
M[i, j] = (M[i - 1, j] and S[i + j - 1] = S1[i - 1]) or
(M[i, j - 1] and S[i + j - 1] = S2[j - 1])
return M[|S1| - 1, |S2| - 1]
The museum would like you to devise an efficient algorithm to determine which guards are assigned to which galleries.
The museum can be represented as a graph G = (V, E) where each vertex represents a gallery and each edge represents a hallway between two galleries. Under this interpretation, the algorithm should create a subset E* of E containing exactly n edges where each vertex in V is adjacent to exactly one edge E*.
The greedy algorithm starts with E* empty and iterates until E* contains n edges. On each iteration, there are two cases to consider:
- There exists an edge (v1, v2) and both v1 and v2 are not yet adjacent to any edges in E*. Add (v1, v2) to E*.
- There exists two vertices v1 and v2 not connected by an
edge in G and neither of which are adjacent to any edge in E*. The
graph
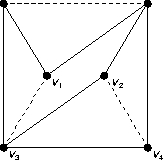
shows an example when n = 3 (dotted edges belong to E*). v1 and v2 are adjacent to a total of at least 2n edges, all of which are adjacent to edges in E* (otherwise case 1 would hold). However there are less than n edges in E*, which means that at least one edge in E* is adjacent to at least three edges that are also adjacent to v1 and v2.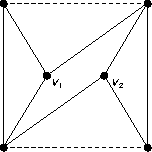
In this case, the algorithm deletes the edge (v3, v4) in E* and replaces it with edges adjacent the vertex pairs (v1, v3) and (v2, v4):