m4_divert(2)
m4_define(_commentnesting, 0)
m4_define(_begincomment,m4_dnl
m4_ifelse(_commentnesting, 0, ))
m4_define(_warning,m4_dnl
_begincomment()This document was created by gen-_name.html Do not edit this document, edit gen-_name.html._endcomment())
m4_define(_hdrs, )
m4_define(_anchor_no, 0)
m4_define(_abs, m4_ifelse(m4_eval($1 < 0), 1, m4_eval(-($1)), $1))
m4_define(hdr,
_warning()
$2
_warning()
m4_ifelse(m4_eval($1 >= 0), 1,
m4_define(`_hdrs', _hdrs`'_anchor_no�$1�m4_translit(`$2', `,', �)�))
m4_define(_anchor_no, m4_eval(_anchor_no + 1))
)
m4_define(usetag, _warning()$2_warning())
m4_define(puttag, _warning()$2_warning())
m4_changecom()
m4_define(sps, $1$2)
m4_define(sbs, $1$2)
m4_define(,_warning()$1_warning())
m4_define($1_warning())
m4_define(itl,_warning()$1_warning())
m4_define(bld,_warning()$1_warning())
m4_define(hrf,_warning()$2_warning())
m4_define(mailat,_warning()hrf(mailto:$1,$1)_warning())
m4_define(nwsgrp, hrf(news:$1, $1))
m4_define(bookref, $1, $2. $3: $4, $5.)
m4_define(i2m,m4_ifelse(
$1,01,January,
$1,02,February,
$1,03,March,
$1,04,April,
$1,05,May,
$1,06,June,
$1,07,July,
$1,08,August,
$1,09,September,
$1,10,October,
$1,11,November,December))
m4_dnl $Revision: 1.5 $, $Date: 1999/12/09 19:16:32 $
CS 512 Test 1
hdr(2, Test 1 - Graph and Geometric Algorithms)
hdr(3, CS 512, Algorithm Design)
-
True or false: every depth-first tree of an undirected graph itl(G) is a
spanning tree over itl(G). Justify your answer.
False. A spanning tree over itl(G) must reach all nodes of itl(G). If
itl(G) is unconnected, no edge can span itl(G)'s separate subgraphs, and no
spanning tree over itl(G) can exist.
-
Let itl(G) be an undirected graph, itl(v) be a node of itl(G), itl(D)t be a
tree generated by a depth-first traversal of itl(G) starting at itl(v), and
itl(B)t be a tree generated by a breadth-first traversal of itl(G) starting
at itl(v). True or false: itl(D)t and itl(B)t will always be identical
subgraphs of itl(G). Justify your answer.
False. Consider the graph itl(G) shown on the left.
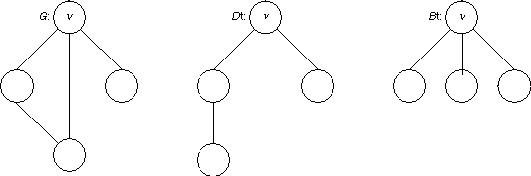
The middle graph itl(D)t is a spanning tree over itl(G) generated by a
depth-first traversal; the right graph is a spanning tree over itl(G)
generated by a itl(B)t breadth-first traversal.
-
A rectangular polygon is a polygon with only horizontal and vertical
sides. Suppose you have to devise an algorithm that accepts a set itl(S) of
points and constructs, if possible, a rectangular polygon from the points in
itl(S). Should you base your algorithm on a circular scan through the points
in itl(S), similar to the circular scan used for the simple polygon algorithm?
Explain.
A circular scan through the points of itl(S) is probably not the best approach
to take. The sides of a rectangular polygon are most conveniently described in
terms of pairs of vertices having identical x or y values. A circular scan
describes vertices in terms of an angle and a distance, and it is not
particularly easy to discover a horizontal or vertical relation between
vertices using angles and distances. Of course, it is always possible to
convert from angles and distances to x-y coordinates (that is, from polar to
rectangular coordinates), but if you're going to do that conversion, you may as
well start with a linear scan parallel to one of the axes and get the x-y
coordinates directly.
-
You are surfing the web and come across a page describing an algorithm that
accepts a set of points itl(S) and indicates whether or not the points in
itl(S) all lie on the same line. Further, the algorithm is guaranteed to have
worst case run-time behavior strictly better than O(|itl(S)|). Does this make
sense to you? Explain.
No. Because itl(S) is an arbitrary set of points, any algorithm that
determines if the points in itl(S) are collinear must examine every point in
itl(S) and so must have at least itl(O)(|itl(S)|) worst case behavior.
This page last modified on 16 i2m(02) 2000.
m4_dnl $Revision: 1.2 $, $Date: 1999/03/12 17:36:48 $
m4_divert(1)
m4_changequote({, })
{m4_define(tblfcntnts,
_toc_tableit(}_hdrs{) _toc_down(_toc_ilevel, _toc_level)
)
m4_define(_toc_tableit,
m4_regexp($1, \([0-9]+\)�\([0-9]+\)�\([^�]+\)�\(.*\),
m4_ifdef(_toc_level, , m4_define(_toc_level, m4_eval(\2 - 1))
m4_define(_toc_ilevel, _toc_level))
_toc_entry(\1, \2, \3) _toc_tableit(\4))
)
m4_define(_toc_down,
m4_ifelse(m4_eval($1 < $2), 1, _toc_down($1, m4_eval($2 - 1)))
)
m4_define(_toc_entry,
m4_ifelse(m4_eval($2 > _toc_level),1,
,
m4_eval($2 < _toc_level),1,_toc_down($2, _toc_level))
_toc_tagit($1, $3)
m4_define(_toc_level, $2)
)
m4_define(_toc_tagit,
-
m4_translit($2, �, ,)
)
}
