Computer Networking

Test 3, 3 December 2013

This test has five questions; answer at least four of them. The test runs one hour, and ends at 5:30.

Up to the first 75 words appearing after a question are taken to be the answer to the question. Words following the 75th word are not part of the answer and will be ignored.

  1. Characterize the most siginficant feature of an mB/nB encoding when m > n.

    An mB/nB encoding with m > n has some m-bit symbols that can't be encoded as n-bit symbols. If m > n, then 2m > 2n; that is, there are more m-bit symbols that there are n-bit symbols.

  2. An Edutella peer-to-peer network has two node layers. The upper-layer nodes are arranged as an n-dimensional hypercube, and the lower-layer nodes have no arrangement. Assuming 1) that the hypercube is complete (that is, there is a node at every hypercube vertex) and 2) each lower-layer node has a single link to a node in the upper layer, what are the minimum and maximum hop counts between any two different lower-level nodes.

    The minimum hop count is two when the two lower-level nodes have a link to the same upper-level node. The maximum hop count occurs when the two lower-level nodes have links to two different upper-level nodes, and the upper-level node addresses in the hypercube differ at every bit, such as 0000 and 1111 if n = 4. In that case, assuming an n-dimensional hypercube, the maximum hop count is n + 2: one hop to get up to the hypercube, n hops to move from one upper-level node to the other, and one hop to go down to the other lower-level node.

  3. Describe two conditions under which Shannon's theorem would indicate that a channel has a data rate of 0 bits/sec. Relate the conditions you describe to a physical realization of the channel (that is, show that the conditions you describe could actually occur in a real channel).

    If channel bandwidth is zero, then Shannon's theorem gives the channel capacity as 0 · log2 (1 + S/N) = 0 bits/sec for any signal-to-noise ratio S/N. Such a condition could occur when the channel has a short or a break, such as when a wire is cut.

    If the signal-to-noise ratio is 0, then Shannon's theorem gives the channel capacity as B · log2 (1 + 0) = B · log2 1 = B · 0 = 0 bits/sec for any bandwidth B. Such a condition could occur when the signal is equal to the noise on the channel; that is, it is impossible to distinguish between signal and noise.

  4. C is a Chord ring storing objects O (movies or documents, for example). Suppose there is a node at every possible address in C's ring. True or false: each node in C will store at most one object O. Justify your answer.

    False, for at least two reasons. First, two different objects Oi and Oj, i ≠ j, could collide in the ring; that is, they could map to the same address, which means they would be stored at the same node. Second, the number of objects that can be stored in C is larger than the number of ring addresses. If the number of objects stored in C is greater than the number of addresses in C, at least two of the objects have collided and there must be a node storing at least two objects.

  5. True or false: If a sender and a receiver communicate over a channel using an NRZI encoding, then the receiver's bit time must be within ±25% of the sender's bit time to avoid decoding errors. Justify your answer.

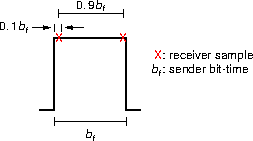
    False. Decoding errors occur if the receiver's bit time is outside the ±25% range, but they will also occur within that range too. Suppose the receiver's bit time is 0.9 of the sender's bit time (that is, the receiver is -10% of the sender), and the receiver samples the signal within the first 10% of a bit. Then the next sample the receiver takes will be from the same bit, a sampling error. If the receiver samples at some other portion of the bit, the sample point eventually drifts back to within the first 10%.

    a short bit-time goes awry

This page last modified on 2013 December 1.