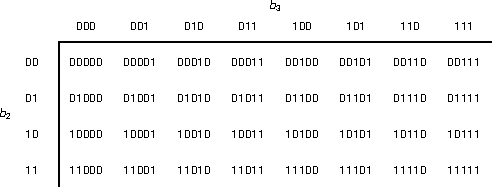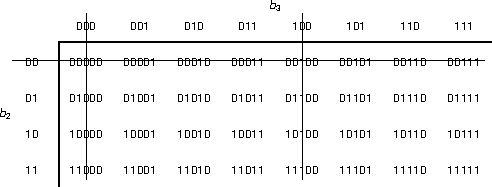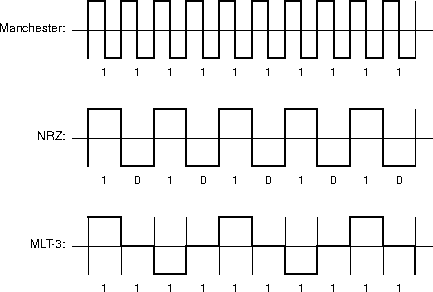Computer Networks, CS 514

Homework 5, 5 November 2013

This assignment is due no later than 6:20 p.m. on Tuesday, 26 November.

This homework assignment has six questions; answer all of them. Answers should no longer than half a page, or around 100 to 150 words. Please site references you use to answer your questions, including the textbooks you’re using.

Your homework may turned-in on paper or via rclayton@monmouth.edu by email. If you mail your assignment, please submit a printable document — a PostScript .ps or PDF .pdf document, for example — and not a source document — a Word .docx or Latex .tex document, for example. Make sure you mail a printable document by the deadline.

  1. Radio antennas work best when the antenna diameter is equal to the wavelength of the radio wave its designed to receive. Determine appropriate antenna diameters for receiving 1) AM, 2) FM, and 3) cell phone transmissions. You may consider a representative frequency from each bandwidth, or a pair of frequencies representing the bandwidth’s frequency range.

    Flipping the relation fλ = c between wavelength (λ) frequency (f) and the speed of light (c) gives the wavelength in terms of frequency and the speed of light: λ = c/f.

    Some representative frequencies (median for AM and FM, lowest for Cell):
    AM1070 kHz
    FM98.1 MHz
    Cell (G3)1.7 GHz
    Plugging these frequencies into the equation (1) gives the wavelengths
    AM:(3 · 108 m/s)/(1.07 · 107 c/s)= 28 m/c
    FM:(3 · 108 m/s)/(9.81 · 107 c/s)= 3 m/c
    Cell:(3 · 108 m/s)/(1.7 · 109 c/s)= 0.18 m/c
    Source: Tanenbaum and Wetherall, Chapter 2.
  2. Develop a 4B/5B encoding with the property that each resulting symbol starts and ends with at most one 0 bit. Your encoding should be as large (encodes as many 4-bit symbols) as possible.

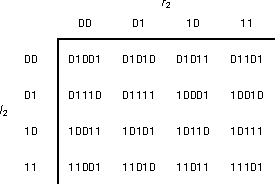
    A 5B encoding can be considered a 2B encoding catenated with a 3B encoding (or vice versa; it doesn't matter as long as the catenation is consistent).

    all 5B codes

    There are eight 5B codes that start with at least two zeros, which isn't allowed by the problem. Of the remaining 5B codes, six end with at least two zeros, leaving a total of 32 - (8 + 6) = 18 valid 5B codes.

    valid 5B codes

    The 16 4B codes can be mapped into 16 of the 18 valid 5B codes in any way convenient; here is a mapping that preserves order (b4 = l2r2):

    a 4B-5B mapping

    Source: sitting and thinking.
  3. What is the minimum bandwidth needed to achieve a data rate of B bits/sec if the signal is transmitted using NRZ, MLT-3, and Manchester encodings? Justify your answers.

    NRZ encoding has worst-case one transition per bit-time (assuming the bit-time interval is closed at the start and open at the end). An NRZ encoding of the worst-case bit stream ...010101... generates a signal of frequency B/2 Hz; a smaller bandwidth would be unable to carry the signal.

    Manchester encoding has worst-case two transitions per bit-time (under the same assumption as NRZ). A Manchester encoding of the worst-case bit stream ...000... (or ...111...) generates a signal of frequency B Hz, the minimum required bandwidth.

    MLT-3 encoding has worst-case one transition per bit-time (under the NRZ assumption). An MLT-3 encoding of the worst-case bit stream ...111... generates a signal of frequency B/4 Hz, the minimum required bandwidth.

    minimum bandwidths

    Source: Tanenbaum and Wetherall, Chapter 2; Lin, Hwang, and Baker, Chapter 2 (MLT-3).
  4. A mobile phone system with square cells

    a triangular cell network

    cannot share frequencies between edge-adjacent cells. Devise a scheme to allocate 840 frequency bands in such a system so that each cell has the maximum number of frequency bands available.

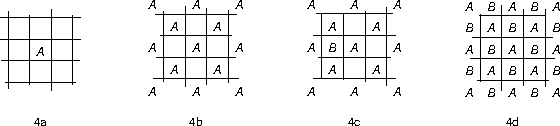
    Start with one frequency A assigned to a cell (Fig. 4a). Assign A to other cells according to the edge-adjacent rule (Fig. 4b). Assign frequency B, different from A, to an open cell (Fig. 4c). Assign B to other open cells according to the edge-adjacent rule (Fig. 4d). All open cells have been filled with two frequencies.

    frequency assignments

    To assign 840 frequencies, treat A and B as sets of frequencies and divide the available frequencies evenly between A and B: A gets the lower 420 frequencies and B gets the higher frequencies, or A gets the odd frequencies and B gets the even frequencies, or similar.

    Source: sitting and thinking.

  5. Evaluate these encoding schemes
    unipolar NRZ-L
    Polar NRZ-L
    NRZ-I
    RZ
    Manchester
    differential Manchester
    AMI
    MLT-3
    with respect to these issues:
    synchronization
    baseline wandering
    DC components.

    AMI:
    AMI’s polar 1s representation make it self-synchronizing with bit-stuffing for 0 runs; bit-stuffing also helps avoid DC components, and polarity provides base-line stability.
    differential Manchester:
    The transitions in the middle of each bit time make differential Manchester self-synchronizing and base-line stable with no DC components.
    Manchester:
    The transitions in the middle of each bit time make Manchester self-synchronizing and base-line stable with no DC components.
    MLT-3
    Different 1 representations allow for self-synchronization, but long runs of 0s require bit-stuffing, and can induce DC components. Polar encoding avoids base-line drift.
    NRZ-I
    Non-return to zero encoding allows for transitionless bit sequences, which require external synchronization and can induce DC components. The polar encoding avoids base-line drift.
    polar NRZ-L
    Non-return to zero encoding allows for transitionless bit sequences, which require external synchronization and can induce DC components. The polar encoding avoids base-line drift.
    unipolar NRZ-L
    Non-return to zero encoding allows for transitionless bit sequences, which require external synchronization and can induce DC components. The unipolar encoding can cause base-line drift.
    RZ
    A transition on every bit means self-synchronization, and polar encoding means no DC components and no base-line wandering.
    Source: Lin, Hwang, and Baker: Chapter 2.
  6. Compare the number of required frequencies and the size of the bandwidth to represent the following signals: 1) periodic analog, 2) aperiodic analog, 3) periodic digital, and 4) aperiodic digital.

    Aperiodic analog or digital signals have a continuous frequency distribution which tend toward zero in amplitude as frequency increases. At low frequencies aperiodic analog signals start low and increase, while aperiodic digital signals start high and decrease.

    Periodic analog or digital signals have discrete frequencies, one per component of a periodic analog signal, and infinitely many, one at each harmonic, of a periodic digital signal.

    Aperiodic analog or digital signals have a high bandwidth requirements given the range of component frequencies. Periodic analog signals have exact bandwidth requirements given by the component frequencies, while an aperiodic digital signal has potentially infinite bandwidth.

    Source: Lin, Hwang, and Baker: Section 2.1.

This page last modified on 2013 December 9.