Computer Networking Lecture Notes
2013 October 24 • Data Link Flow & Error Control
Outline
- Error detecting codes.
- Parity, checksum, cyclic redundancy checks.
- Error correcting codes.
- Sliding-window flow control.
Errors
- An error occurs when a bit “spontaneously” changes value: 0 → 1 or 1 → 0.
- A bit string undergoes an error burst of length n at bit
i when
- bits i and i + n - 1 change value, and
- bits i + j, 0 < j < n - 1, change value with probability p.
- 010000 → 000101, i = 1, n = 5, p = 0.3.
- Frequently i is ignored and p = 0.5.
Error Detection
- Error detection is most useful when
- Error rates are low (≥ 109 bits/error).
- Errors can be ignored.
- Retransmission is cheap.
Parity
- Parity deals with even or odd 1-bit counts.
- A bit string has an even or odd 1-bit count.
01000010 2 1-bits even parity 01011000 3 1-bits odd parity - A bit string’s parity bit is the value giving the bit string
even parity.
01000010 parity bit = 0 01011000 parity bit = 1
Parity Error Detection
- Append a parity bit to a bit string; the result always has even parity.
- A string + parity with odd parity indicates an error.
- Parity can detect single-bit errors.
- Or an odd number of single-bit errors
010000100
010100100
010000000
010000101
010000100
000010000
100010010
101010011
More Parity
- Parity doesn’t detect an even number of errors.
- Add more structure by using smaller groups and more parity bits.
- Even numbers of errors in a group still go undetected.
|
|
010000100 |
|
|
0100001011 0000000011 1010000011 1010100001 |
Interleaving
- Add even more structure by interleaving, not grouping, bits.
- K-bit interleaved parity - k parity bits, one for each
kth bit.
- Any one of the parity bits is enough to signal an error.
|
|
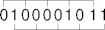 0000000011 1010000011 1010100001 |
Checksums
- Use arithmetic for even more structure.
- Group the bit string into k-bit values.
- Sum the values to get a k-bit checksum.
- Append the checksum to the bit string.
- “Checksum” often refers to any error-detection value.
- Checksums differ in handling the carry-out bit.
Internet Checksums
- The Internet checksum (rfc 1071) is
- the one’s-compliment of
- the sum of 16-bit one’s compliment values.
- The checksum IP header field is part of the checksum.
- The sender zeros it out.
- The receiver includes it in the checksum.
- A successful checksum produces -0.
More Structure
- Moving from parity bits to arithmetic adds structure.
- Adding more arithmetic adds more structure.
- An n-bit message can be represented as an n-1 degree
binary coefficient polynomial.
- Given M = bn-1\(\cdots\)b1b0,
- get M(x) = Σ0 ≤ i < n bixi.
- The sender and receiver exchange binary coefficient polynomials.
Example
- Let M be 10011010,
- then
M(x) = b7x7 + b6x6 + b5x5 + b4x4 + b3x3 + b2x2 + b1x1 + b0x0 = 1x7 + 0x6 + 0x5 + 1x4 + 1x3 + 0x2 + 1x1 + 0x0 = x7 + x4 + x3 + x
Fun Division Facts
- Suppose a/b = q remainder r, 0 ≤ r <
b.
- Then a = q*b + r, and
- (a - r)/b = q remainder 0.
- For example
25/4 = 6 remainder 1
25 = 4*6 + 1
(25 - 1)/4 = 24/4 = 6 - Similar fun facts hold for polynomials.
Polynomial Error Detection
- Sender and receiver agree
- on a check polynomial C(x) of
degree k.
- K is the number of error checking (redundant) bits.
- to only send messages (polynomials) evenly divisible by C(x).
- on a check polynomial C(x) of
degree k.
- If C(x) doesn't even divide the received message (polynomial), errors occurred during transmission.
Evenly Divisible Polynomials
- A message polynomial M(x) may not be evenly divisible by C(x).
- Not to worry:
- Add k extra bits to M(x): M'(x) = M(x)xk.
- Subtract the remainder of M'(x)/C(x) from
M'(x) to get M''(x).
- C(x) evenly divides M''(x).
- Send M''(x).
Cyclic Redundancy Check
- Polynomial-based error detection is known as cyclic redundancy checking (CRC).
- CRC is a powerful error detection technique.
- Few check bits protects many message bits.
- k = 32 and n = 12,000 (1,500 bytes).
- Few check bits protects many message bits.
Selecting C(x)
- Check polynomial properties determine CRC error-detection capabilities:
- All single-bit errors when the xk and x0 terms have coefficient 1.
- All double-bit errors when C(x) contains a factor with at least three terms.
- Any odd number of errors when C(x) contains the factor x + 1.
- Any error burst of length less than k bits.
Error Correction
- If
- error rates aren't low (≤ 106 bits/error), or
- errors can't be ignored, or
- retransmission is expensive, then
- error detection doesn't do a good enough job.
- Or fix the errors when detected.
- This is known as forward error detection.
Redundancy
- Undoing errors requires extra information, meaning extra bits.
- An m-bit message uses r bits of redundancy.
- This is an (n, m) code, n = m + r.
- The n-bit result is a codeword.
- The code rate = m/n measures redundancy.
- High error rates, code rate ∼ 0.5.
- Low error rates, code rate ∼ 1.
Distance
- Count the 1 bits in the exclusive or of the codewords.
- The Hamming distance between two codewords is the number of
different bits.
- 01000010 and 01011010 have Hamming distance 2.
| Two codewords differ in some number of bits. |
|
Errors and Distances
- Two codewords with Hamming distance d require d single-bit
errors to change one into another.
01000010 → 01010010 → 01011010 01000010 ← 01010010 ← 01011010
- A code's Hamming distance is the smallest Hamming distance between any
two codewords in the code.
for all i, j : min Hamming(ci, cj)
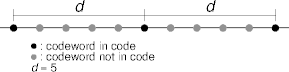
Sparseness
- An (n, m) code contains codewords in inverse proportion to its
Hamming distance.
- The larger the Hamming distance, the fewer the codewords.

Error Detection and Correction
- A code with Hamming distance d can
- detect up to d - 1 errors in a codeword.
- correct up to ⌊(d - 1)/2⌋ errors in a codeword.
Flow Control
- Faster senders may swamp slower receivers.
- Resulting in inefficient communication.
- Flow control throttles the sender back to the receiver's rate.
- Preferably just this side receiver overload.
- Link efficiency is not as important.
- Flow control and reliability are different but related techniques.
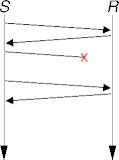
Stop And Wait
- Stop and wait is the simplest flow control mechanism.
- The sender has at most one unacknowledged frame in flight.
- The next frame is sent on receiver ack.
|
|
|
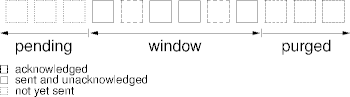
Sliding Window
- Stop and wait can be inefficient: frm/rtt bit/sec.
- The sliding window protocol keeps n unacknowledged frames
in flight.
- N is the window size.
Sliding-Window Efficiency
- Sliding-window link utilization is n*frm/rtt bit/sec.
- N is the window size.
- The receiver ack sequence is known as an ack clock.

Sequence Numbers
- Several unacknowledged frames and frame loss makes anonymous acknowledgments ambiguous.
- Sequence numbers resolve the ambiguity.
- By making acks specific to a frame
|
|
|
Summary
- Errors in transit may be detected and possibly corrected.
- Depending on costs (extra bits, missed errors) and benefits (faster cheaper recovery).
- Flow control rate matches end-points.
References
- Performance of Checksums and CRCs over Real Data by Jonathan Stone, Michael Greenwald, Craig Partridge, Jim Hughes in IEEE/ACM Transactions on Networking, October, 1998.
- Cyclic Redundancy Code (CRC) Polynomial Selection For Embedded Networks by P. Koopman and T. Charkravarty, International Conference on Dependable Systems and Networks, June 2004.
| This page last modified on 2012 October 25. |