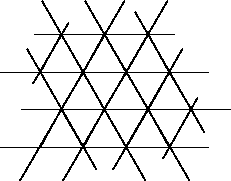Re-arrange λf = c to get f = c/λ. From c = 3×108 m/sec and λ = 3×10-2 m/cycle get
(3×108 m/sec)/(3×10-2 m/cycle) = 3 × 1010 m/cycle = 30 GHz.From λ = 5 m/cycle get
(3×108 m/sec)/(5 m/cycle) = 60×106 m/cycle = 60 MHz.
The answers, approximately verbatim, and in no particular order:
-
Speed of Light = Wavelength*Frequency
To solve for frequency: \ Frequency = Speed of Light/Wavelength (in nm) \ Speed of Light = 3 * 10^8 m/s
1 cm = .01 m(3*10^8)/100000001 = 30 MHz \ (3*10^8)/5 = 60000000 Hertz*1.0 × 10^-6 = 60 MHz
60 MHz - 30 MHz1: This is not the right value for 1 cm.
-
Frequency, f = c/l where c is speed of light, i.e., 3*10^8 m/s \
Frequency of radio wave with 1 cm (i.e., 0.01m) diameter is f = c/l =
3*10^8/0.01 = 3 × 10^10 = 30 Ghz \
Frequency of radio wave with 5m diameter is f = c/l = 3 × 10*8/5 = 6
× 10^7 = 60 MHz \
The cover range is from 60 MHz to 30 GHz. \
Reference: Class Notes
-
Frequency = the speed of light/wavelength. Based on that formula (and
keeping wavelengths in meters), the minimum frequency would be 299,92,458 m/s
/ 5 m = 59,958,491.6 Hz, and the maximum frequency would be 299,792,458 m/s /
.01 m = 29,979,245,800 Hz. The range is approximately 60.0 MHz to 30.0 GHz.
Source: HTTP://www.tomcarpenter.net/2009/11/21/rf-wavelength-calculations-for-wireless-networks/
-
Freq = C/W where C: speed of light. W: wavelength. \
Convert 1 cm to m → 1 cm = 0.01 m
For diameter of 1 cm: \ Freq = (3 × sup(10, 8)/0.01 \ Freq = 3 × sup(10, 10) = 30 GHz
For diameter of 5 m: \ Freq = (3 × sup(10, 8)/5 \ Freq = 6 × sup(10, 7) = 60 MHzThe cover range is from 60 MHz to 30 GHz.
-
Given, \
Diameter of the antenna = wavelength of the radio wave i.e. 1 cm to 5 m \
We know that,
Frequency(f) = speed of light(c)/wavelength(l)
Now for 1 cm, f = c/l = 3 × 10^8 / 0.01 = 3 × 10^10 = 30 GHz Now for 5 meters, f = c/l = 3 × 10^8 / 5 = 6 × 10^7 = 60 MHz Hence the frequency range that these radio antennas cover are from 60 MHz to 30 Ghz.
a) A river rapids is simplex because transport can only go downstream. b) A canal is half-duplex because ships can go up-grade or down-grade, but only one way at a time. c) A wide river is full-duplex because it supports simultaneous two-way traffic. d) A water fall is none of these because it supports no (useful) transportation at all.
The answers, approximately verbatim, and in no particular order:
-
Simplex: One-way streets are simplex because they allow traffic in only one
direction with no change in direction allowed.
Half-duplex: Street Lights with delayed green lights (such that one side is green first, then it switches to red while the opposite side becomes green) is an example of a half-duplex system because it allows traffic to flow both ways (e.g. across the highway), but only one way at a time.
Full-duplex: Regular traffic lights are full-duplex because when the light is green, traffic can flow from both directions at the same time (e.g., crossing the highway at the same time).None of the above: A traffic circle is none of the above because it allows for multiple directions to be traveled simultaneously with both inputs and outputs; alternatively, a road closed for maintenance is none of the above because there is no traffic flow in any direction.
-
a) A simplex network is a service that provides one-way communication. A
non-electrical system for the simplex is the radio broadcasting1 where the radio device obtains
the signals from the broadcasting source.
b) A half-duplex network is a two-way communication but cannot communicate simultaneously, they can communicate one at a time in one direction. An example for this is a walkie-talkie where when one person uses the device the other person has to just hear and vice versa.2
c) A full-duplex communication is a two-way communication achieved over a physical link that has the ability to communicate in both directions simultaneously. A example for this is a telephone line which has two lines one for transmitting and the other for receiving which means both the persons can talk and listen at the same time.d) Examples where the systems don't use simplex half-duplex and full-duplex are repeaters and modems.
1: How is radio broadcasting non-electrical?
2: Non-electrical?
-
- Simplex Transmission
Data in a simplex channel is always one way. Simplex channels are not often used because it is not possible to send back error or control signals to the transmit end.
Examples of simplex channels: In tankless water heater, water goes in one direction inside the heater. In a one-way street, vehicles move in one direction.- Half-Duplex Transmission
A half-duplex channel can send and receive, but not at the same time. Here we need to switch between transmit and receive mode. It is like a one-lane bridge.Examples of half-duplex channels: In a single railroad track, trains can move either forward or backward at a time.
- Full-Duplex TransmissionData can travel in both directions simultaneously. There is no need to switch from transmit to receive mode like in half-duplex. It is like a two-lane bridge.
Examples of full-duplex: In a two-lane road, two vehicles can move in both directions at the same time.- Any other system goes under one of these categories.
(Tanenbaum, Computer Networks, chapter 2) -
a) Simplex example is speech because the person who is giving speech is the
only one who talks and all others listen to it.3
b) Half-duplex example is satellite phones example Iridium operates a one-way pager service as well as the call alert feature.
c) Duplex example is cellular phones because both sides can talk at the same time.d) [ not answered ]
3: How polite you are.
-
A one-way street can be considered simplex because cars can only go one way
on it, there is no chance of going the other way. A bus can be considered
half-duplex transmission, people can get on or off the bus but not at the
same time; people get off, and then people get on. A two-way street can be
considered full duplex because cars can come and go at the same time. A
closed street would be none of a, b, and c because no cars can come or go.
Describe the topology of each of the networks. Justify your answers.
network best average worst A 2 2 2 B 1 n/2 n/2 C 1 1 1
Network A is a star network with one hop going to the hub and the other hop to the destination. Network B is a bi-directional ring network. Network C is a fully connected network.
The answers, approximately verbatim, and in no particular order:
-
Network A could be described as a linear topology consisting of three
nodes X, Y, and Z1 (and therefore, two hops from X to Z via Y)
linked together in a line. It would always take two hops to travel from
X to Z (or from Z to X) since y is the intermediate node.
Network B could be described as a tree where the best case is one hop to an ancestor/descendant and the worst case is traveling from the root to a leaf node (n/2 hops).2
Network C could be described as a central hub surrounded by nodes in a bicycle-wheel pattern where the nodes are linked with the central hub with spokes (the spokes being the network path). It would take one hp from the center to any node in the network.1: It could, but n is arbitrary.
2: But trees aren't linear; they're logarithmic.
-
Three networks each contain ‘n’ nodes. \
The first is star topology with a central router because in a start topology,
transmission path from one node to other node will be ‘2’ in all cases
(through central router), the second is a bidirectional ring because in
bidirectional ring topology, transmission path from one node to other node is
‘1’ if nodes are adjacent and ‘n/2’ if nodes are far away, and
the third is fully interconnected (every node is connected to every other)
because in a fully connected topology, the transmission path from one node to
other is ‘1’ because all nodes are connected to all other nodes.
star - 2, 2, 2 hops (best, average, worst) \ ring - 1, n/2, n/2 \ full - 1, 1, 1
-
[ not answered ]
-
First case, \
Now the first network is having a path equal to 2. Hence the packet goes
from the originating computer to the switch, then from the switch to the
destination computer. During this process 2 hops take place.3
Second case, \ The second will have a best path equal to 1 and a worst path equal to n/2 and an average of (n/2)/2. Hence the worst path is equal to n/2 because the farthest a packet will have to travel is equal to half the total nodes because it is a bidirectional ring. Hence we assume the average.
Third case, \ Now the third which is an interconnected network will have a best, average and worst case of 1. Because all of them are connected to each other, there is no hopping at all and each computer can connect to any other computer directly.3: What's the network topology?
-
A 2 2 2
This represents a star topology.
In this network, each node is connected to other nodes via central node called hub or switch, and a node gets to any other node in this network via the hub or switch.B 1 n/2 n/2
This represents a ring topology.In this network, each node is connected to two other nodes in the same signal path, and the path forms a circle.
C 1 1 1This represents a fully connected topology.
In this network, each node is directly connected to all other nodes.(source: http://computer.howstuffworks.com)
cannot share a frequency band between edge-adjacent cells. Devise a scheme to allocate 840 frequency bands in such a system so that each cell has the maximum number of frequency bands available.
Consider a cell C and its three surrounding neighbors. Each frequency used in C is unavailable for its neighbors, and each frequency used by a neighbor is unavailable to C, but is available to C's other neighbors. By this argument C gets half the frequencies and each of its neighbors get the other half. Because this argument doesn't distinguish among the neighbors, it can be repeated endlessly on the plane.
The answers, approximately verbatim, and in no particular order:
-
Take six triangular cells around a point as a hexagonal group of cells.
Every other cell should contain a frequency band.1 Repeat this pattern for all neighboring groups of cells
throughout the network. Once the network is populated with these neighboring
groups, each empty cell will have access to three frequency bands.2
1: The same frequency band?
2: Just three frequencies per cell? Is that the maximum?
-
[ not answered ]
-
In the following figure, each cell has three neighbors. When a cell uses
frequency of group A, its two neighbors can use frequency of group B (as
shown below). Consequently, only two group of frequencies are needed, and
number of frequencies that can be used will be: \
frequency bands/number of group \
840/2 = 420 frequencies (http://searchnetworking.techtarget.com)
[ diagram ]
-
Each cell has three other adjacent cells, in a triangular grid. \
So it has to avoid any frequency that any of these cells use. \
This pattern can repeat, and cover the plane endlessly, so these three other
cells have to avoid each of the others, but no more. \
The above figure makes this clear, and shows that there are for “kinds”
of cells. For each cell to have the same number of frequencies (so that a
user has the same sort of experience no matter what cell they are in). \
Hence they all have to have the same number of frequencies, i.e. thus
840/4 = 210
The obtained answer is from the assumption that no two cells that are adjacent to the same cell can re-use frequencies.33: Does this provide each cell with the maximum number of frequencies?
-
There can be at least three frequency groups A, B, and C.
Dividing the total available frequencies by three gives us 840/3 = 280
frequencies for each cell.4
4: But is that a maximum for each cell?
Because 125 usec is 1/8th of a msec, which allows a 1 byte/msec (or a 1k byte/sec) sample rate.
The answers, approximately verbatim, and in no particular order:
-
This corresponds to a sampling rate of 8000 samples/sec. According to the
Nyquist theory, this is the sampling frequency needed to capture all the
information in 4 kHz channel. (HTTP://searchnetworking.techtarget.com)
-
A sampling time of 125 usec corresponds to 8000 samples per second.
According to Nyquist theorem, this is the sampling frequency needed to
capture all the information in a 4 kHz channel, such as a telephone signal. \
Reference: Tanenbaum and Wetherall
-
A PCM system digitally represents analog signals. Analog signals are
digitized by codecs and the codecs make 8000 samples per second which is equal
to 125 usec. The Nyquist theorem states 125 usec is enough to capture all
the information from the 4 kHz telephone bandwidth.
Source: Computer Networks - Tanenbaum and Wetherall
-
Given a sampling time of 125 usec,
which corresponds to 8000 samples per second.
Now according to the Nyquist theorem which states that,IF a function x(t) contains no frequencies higher than B Hertz. It is completely determined by giving its ordinates at a series of points spaced 1/(2B) seconds apart.
Hence this is the sampling frequency that is needed to capture all the information in a 4-kHz channel, such as a telephone channel. Actually the nominal bandwidth is some what less, but the cutoff is not sharp. -
The Nyquist Sampling theorem ("The minimum data rate D (in bps) of a
communication channel (Channel capacity) with bandwidth B where we can
recognize K levels in the signal is D= 2B log2 K) shows how to
sample the analog signal in PCM. It says that it's possible to reconstruct a
signal from 2B samples. If a telephone channel is used (4 kHz), then 8000
samples are needed (2*4000 Hz). Applying the formula with 256 amplitude
levels yields a data rate of one byte every 125 usec.
HTTP:www.ics.temple.edu/~giorgio/cis307/readings/datatrans.html