Ports are the other IPv4 address space. An IPv4 address combined with a port is a 32 + 16 = 48-bit address. It seems unlikely that a single host would exhaust the port address space, as that would require that it be running 65,000+ processes at one time, but note that the 48-bit address space has the same problem as the class-based IPv4 address space: it is inefficiently distributed in the network and difficult to share. Hosts that need only a few addresses still gets a full compliment of them, and can't easily make the extras available to hosts that may need more addresses.
The answers, approximately verbatim, and in no particular order:
-
Besides ICANN, network address translation (NATs) can be used to connect
computers to the Internet.1 NATs modify a single, unique IP address such
that a group of computers can connect to the Internet.2 NATs will help alleviate the IPv4 exhaustion crisis insofar as IP
addresses are needed within home networks and other such setups that lend
themselves to the NAT “Band-Aid.” If unique sources continue to arise
and require unique IP addresses (which is likely in this day and age), then
the NAT solution will not be able to facilitate, and the “address
space” will run out. It is currently being used as a bridge to smooth the
transition to IPv6, which will have a much larger address space, and it seems
to be a patch to the problem that will allow humanity to limp into the realm
of IPv6 where the Internet can grow and thrive successfully
again.3
Source: http://computer.howstuffwords.com/nat.htm
Source: http://www.pjsip.org/pjnath/docs/html/group__nat__intro.htm
1: How can ICANN be used to connect computers to the Internet?
2: How do NATs do that?
3: This answer is too long.
-
Given the address span has run out: ICANN has no unallocated IPv4 addresses
to hand out and there is another address space that could also run out
associated with the IPv4.4
Then it is the NAT device that is responsible for establishing services from
internal[?] addresses to extend devices.5 Will not work then[?] the translation[?] session6 is less than 64511 then it is inadequate if the
IPv4 pool run out.
4: Are you restating the question here, or is this part of the answer?
5: How does a NAT device do this? And what are external addresses? And what does it mean to extend devices?
6: What is the translation session?
-
The second address space that is associated with IPv4 is subnets. This
allows the addresses to be split into multiple parts for internal use as
multiple networks, and still acting as a single network to the outside
networks. Subnet masks can run out, however there are two options if you run
out of a subnet mask. You can change it to allow for more devices7 or add a
router to increase the IP address range, which will basically allow the user
to start over with a new subnet mask.8
These two options make it highly unlikely to run out of subnet masks.
Source: Computer Networks --- Tennenbaum and
http://www.russbelew.com/pages/networking_subnets.aspx
7: Change what to allow for more devices? And what are the changes?
8: Do routers do that? How?
-
Another address space associated with IPv4 is Port addressing. A port is a
16-bit identifier assigned to processes. So there are 2^16 ports available.
There are 65,535 ports available for TCP and UDP connections in TCP/IP. The
first 1024 ports are reserved for specific services and protocols. So 65535
- 1024 is still 64511 ports. Dynamic communication is any sort of network
communication that doesn't already have a port specifically reserved for
sending or receiving it.
There's a possibility of running out of ports, it happens because an
application has been grabbing those ports and not releasing them properly.
So, over time, it uses up more and more ports from the dynamic range until we
run out.
TCP/IP port exhaustion is more likely to occur under high load conditions
than under normal load conditions.
On Windows Server 2003 and Windows XP the default range of ephemeral ports
used by client applications is from 1025 through 5000. Under certain
conditions it is possible that the available ports in the default range will
be exhausted.
References: Class Notes & Textbook
-
TCP or UDP if transmission session one less than 645119 then it is inadequate f10 if the IPv4 pool runs out.
So NAT device which is responsible for establishing sessions from internal
addresses11 to internal device
doesn't work if transmission session one less than 64511.12
9: What does it mean for a TCP or UDP transmission session to be one less than 64511? And what's so special about 64511?
10: What is inadequate?
11: What are internal addresses?
12: Did you argue somewhere in this answer why establishing sessions from internal addresses doesn't work?
-
The second address is IPv6. IPv6 is a new version of the Internet protocol
which was designed to replace the old protocol which is IPv4 since it ran out
of addresses.13 IPv6 was
designed by the Internet Engineering Task Force which is known as IETF. It
is known that every technology has a life span and one technology will not
last forever. When IPv4 was first designed, it was unlikely to think about a
problem like running out of IPv4 addresses since IPv4 was offering addresses
up to 4.3 billion addresses. In 2011, world had to accept the fact that 4.3
billion addresses were exhausted. Fortunately, the replacement version of
IPv4 offers addresses up to 3.4 x 10 sup 38 addresses or in other words 430
times 10 to the 36th power.14
As we mentioned before, every technology has a life span, and has IPv4 ran
out of addresses, IPv6 would too but not in the near future. IPv4 took 3
decades to run out with 3.4 billion addresses. Meanwhile, technology and
devices 3 decades ago are not the same as today and more decades later.
researches show that there were 10 billion devices connected to the Internet
in 2011, and there will be 25 billion in 2020. (Dave Asprey
cloud.trendmicro.com, 25 Sep. 2012. Web).
That means there will be 3 devices for each person on Earth in 2020. What if
we consider people and devices in 2030 or 2050? The number and ration will
be increasing dramatically. However, if that ratio will not change, we will
be using IPv6 for 2.55e31 more years.15
13: But the question asks about IPv4.
14: Is this part of the sentence necessary?
15: This answer is way too long.
-
The other address space associated with IPv4 is IPv6 (Internet Protocol
version 6).16 IPv6 is
the newest version of the Internet protocol, and it is growing to replace the
IPv4 because IPv4 is exhausted of the Internet growth and it is not longer
capable to deal with that. So, IPv6 was developed to deal with the running
out of IPv4 addresses.
IPv6 would be run out as same as IPv4, but by different reasons, which are:
* Most of ISPs around the world are not interested in IPv6 because there is
not need to it as long as IPv4 can get the job done.
* Rare uses of IPv6 within places around the world such as Europe and
Asia.
* Implementing IPv6 is difficult or even impossible sometimes because of
some consequences such as changing the Network Layer protocols, changing
Application layer protocols, and replacing the foundations.
Reference is (Computer Networking, a Top-Down Approach, pages 320--326).
16: In what way is IPv6 associated with IPv4?
A gateway with a maximum throughput of 2 x 10 sup 6 packets/second handles 1.5 x 10 sup 6 packets in (1.5 x 10 sup 6)/(2 x 10 sup 6) = 0.75 sec. A packet arriving at a gateway under average offered load can expect to spend 0.75 sec reaching the other side of the router. Miami and Seattle are approximately 2,700 great-circle miles apart. Light travels through fiber at 124,000 miles/sec, which means a packet spends somewhere around 2,700/124,000 = 0.02 sec in the cable. The fraction of time a packet spends in gateways when going between Miami and Seattle is (0.75 times 10)/((0.75 times 10) + 0.02) = 99.7%
The answers, approximately verbatim, and in no particular order:
-
So p = 1.5/2 = 0.75
Each packet experiences a delay four times that in an idle system.1
So the time in idle system is 500 nsec or 0.5 usec. Here it is 4 x 0.5 = 2
usec.
As these are 10 gateways, total time taken is 2 x 10 = 20 usec.
1: Why is that true? Is there an idle system somewhere in this problem?
-
A gateway can process a maximum of 2 million packets/sec,
i.e. μ = 2 million.
the average offered load for gateway is 1.5 million packets/sec
i.e. λ = 1.5 million. So
\[P = {\lambda \over \mu} = {1.5 \over 2} = 0.75\]
From queuing theory, each packet experiences a delay 4 times in an idle
system,2
i.e., the latency[?] in an idle system is 500 nsec.3 Hence here it is 500 nsec t × 4 = 2 usec.
Now the packet is passing through 10 gateways so the total transit time sent
through the gateways is 2 × 10 = 20 usec
2: What? If the system is idle, why would a packet experience any delay? And is the system described in the question idle?
3: Why 500 nsec?
-
Data we have:
* Maximum number of packets (M) : 2,000,000 packets/sec
* Average number of packets (A) : 1,500,000 packets/sec
* Number of gateways (NG) : 10
Formula: 1/(1 - (A/M))*NG
1/(1 - (A/M))*NG
= 1/(1 - (1500000/2000000)
= 4 microseconds4
4*10 = 40 microseconds
4: Why is this microseconds?
-
1 gateway, maximum of 2 million packets/second \
average offered load for one gateway, 1.5 million packets/second \
One packet passes through ten gateways
-
If the packet arrives at a gateway that is beyond its 2 million packet/sec
limit, it will be forced to wait until the gateway frees up space and is able
to push the packet through to the next gateway. Since the average offered
load for the gateways is 1.5 million packets/sec, this overload issue
(theoretically) will not occur as frequently.5 If 1.5 million packets/sec is the average workload, it is
possible to assume that maybe three of out the ten gateways are overloaded at
the time of the packet's receipt.6
If this scenario is true, the packet will spend at least one second at each
of the three gateways waiting to be processed.7 That time plus the standard time that
it takes each packet to be processed by the gateway is the total amount of
time that it spends within the gateways.8
This number divided by the total amount of time it takes the packet to travel
from Seattle to Miami is the fraction of time it spends in the gateways.
Source: Class lecture 10/03/2012.
5: Or at all, so why bring it up?
6: Why is that assumption valid?
7: What happens to the packet at the other seven gateways?
8: How much time is that?
-
As mentioned, the gateway processes 2 million packets/sec as a Maximum, and
the average offered load for gateway is 1.5 million packets/sec as a Minimum.
Also, there are 10 gateways.
To calculate the packet's total transit time through one gateway, we should
divide the Minimum process on Maximum process.9 Then, we should multiply the
packet's total transit time through one gateway in how many gateways.
The packet's total transit time through (n) gateways
= (Min/Max)*(n) Gateways
= (1.5 million/2 million)*10
= 7.5 seconds
The total transit time for a packet through 10 gateways is 7.5
seconds.10
9: Why? What are the units in the result? What does it represent?
10: Is that what the question asked for?
-
Given a gateway can process 2 million packets/sec = u \
The load offered to it is 1.5 million packets/sec = lambda \
From queuing theory, p = u/lambda = 2 x 10^6/1.5 x 10^911 = 0.75 \
The time in an idle state12 is 500 nsec, here it is 2 usec.\
The route from source to destination contains 10 routers \
So, time spent by a packet in gateways is 10 x 2 usec = 20 usec.
Reference: textbook
11: 9 or 6?
12: What idle state?
The Gobi desert is 5 times 10 sup 5 square miles. A square mile is 27,878,400 square feet, and the Gobi desert is 5 times 10 sup 5 times 27,878,400 = 1.4 times 10 sup 13 square feet. Assuming the desert is uniformly 10 feet deep, the Gobi desert is 1.4 times 10 sup 14 cubic feet. A grain of sand is 3.5 times 10 sup -5 cubic feet, and there are (1.4 times 10 sup 14)/(3.5 times 10 sup -5) = 4 time 10 sup 18 grains of sand in the Gobi desert. There are 2 sup 128 ≈ 3.4 times 10 sup 38 IPv6 addresses, and each grain of sand gets (3.4 times 10 sup 38)/(4 times 10 sup 18) ≈ 2.5 times 10 sup 18 IPv6 addresses. Sources: Wolfram alpha - How big is the gobi desert? How big is a grain of sand?
The answers, approximately verbatim, and in no particular order:
-
Assuming that the Gobi desert covers 1.3 million square kilometers, the
conversion to square meters yields 13 m^2. Desert sand heights range from 0
to 100 feet typically, so assuming the ceiling value of 100 feet (converted
to 30.48 meters), the volume of the Gobi desert is (very roughly)
1,3000,000,000,000 m^2 * 30.48 m, which equals 39,624,000,000,000 m^3.
Assuming a 1mm diameter for an individual grain of sand, there would be
approximately 1,3000,000,000 grains of sand in one cubic meter. Multiplying
this number by the approximate volume of the Gobi desert. Given that there
are 340,282,3666,920,938,463,374,607,431,768,211,456 addresses available in a
128-bit space, addresses divided by grains of sand results in 6.61 x 10^15
addresses per grain of sand.
Source: http://www.why.is/svar.php?id=4803
Source: http://www.quora.com/How-deep-does-the-sand-go-in-a-desert
Source: http://www.freebsd.org/doc/handbook/network-ipv6.html
Source: http://gobidesert.org/content/facts
-
Gobi area is 1,295,000 square kilometers. Average diameter of a grain of
sand is 1mm therefore best estimate is 1645 million billion grains. IPv6
uses 1028-bit addresses, allowing 2^128, or approximately 3.4x10^38
addresses. Number of IPv6 addresses available are 3.4x10^38 addresses. So
each grain gets (3.4x10^38)/(1645x10^15) addresses = 0.00206686 x 10^23
addresses.
Reference: \
Wikipedia for Gobi desert area \
Text book for IPv6 addresses number
-
[ unanswered ]
-
No of addresses = 2128
No of grains = 10191
So each grain gets
\[ \frac{2 ^ {128}}{(2)^{19}(10)_^{19}} = \frac{2 ^ {119}}{(10)_^{19}}. \]
1: From where did this number come?
-
* First Step:
The size of Gobi desert in cubic kilometer:
Length x Width x Height
1500 x 800 x 1 = 1200000 km sup 3
* Second Step:
Convert the size of Gobi desert from km sup 3 to mm sup 3
Size = 1.2e24 mm sup 3
* Third Step:
In average, we have 20 grains per centimeter.
(Since we have a minimum of 15 grains and a maximum of 25 grains)
In cubic centimeter that equals: 20 x 20 x 20 = 8000 cm sup 3
In cubic millimeter: 8000 x 1000 = 8000000 mm sup 3
Estimated number of stand grains in Gobi desert is: 1.2e28 x 8000000 =
9.6e30
* The Result:
Number of IPv6 per grain = 3.4e38/9.6e30
We get: 35416666.6 IP per grain.
(http://mathdude.quickanddirtytips.com. 20 July 2012. Web)
-
Total number of addresses that IPv6 can hold is 2^128 = 3.4 x 10^38
Estimated number of grains on earth = 7.5 x 10^182
So each grain gets
3.4 x 10^38/7.5 x 10^18
= 34 x 10^39/75 x 10^19
= 0.5 x 10^20
= 5 x 10^19 IP addresses approximately.
2: From where did this number come? And is that what the question asks about?
-
Firstly, let's assume how many grains of sand in the Gobi desert: The Gobi
desert area is about 1,295,000 square km, and my assumption for the diameter
of a grain of sand is about 1 mm. Then, the grains of sand per km are about
1,000,000 grains in 1 km. Finally, to assume how many grains of sand in Gobi
desert I should multiply the Gobi desert area in how many grains of sand per
km.
Grains of sand in Gobi desert
= the Gobi desert area * Grains of sand per km
= 1,295,000 * 1,000,000
= 1.285e+12 grains of sand in the Gobi desert
Secondly, IPv6's address space size is about 3.402823669 x 10^38 =
3.4028237e+38.
Lastly, to know how many IPv6's addresses that each grain of sand gets, I
divided the IPv6 address space size on now many grains of sand in Gobi
desert.
Each grain of sand gets
= IPv6's address space size/Grains of sand in Gobi desert
= 3.4028237e+38/1.925e+12
= 2.6276631e+26
Each grain of sand gets 2.6276631e+26 IPv6 addresses.
References is (www.en.wikipedia.org, IPv4 address exhaustion / IPv6 / Gobi
desert).
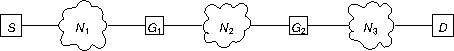
drop packets with probability p; the networks Ni always deliver a packet from one edge to the other (they never lose packets). If host S sends a packet to host D and doesn't get a reply from D within some time, it resends the packet, and keeps resending the packet until it gets an reply. D only sends packets to S in reply to packets received from S; D never spontaneously sends a packet to S. Counting each network transit has a hop, what is the average (mean) number of
- hops made by a packet sent by S?
- times a packet is sent (initial + retransmissions) by S?
- hops made by a packet received by D?
As always, the trick to probability problems is to count the right things. In this case, if a packet drop is represented by 0 and a packet pass-through is represented by 1, then a successful packet delivery is a sequence of 0s and 1s such that the last two digits are 11 and every other 1 in the sequence appears between two 0s or starts the sequence. Given that every successful transmission ends with 11, we can ignore them and remember that they're there. A n-digit sequence with i 1s has probability (p sup i)((1 - p) sup (n - i)) assuming each gateway makes its drop-pass decision independently (which is a convenient but questionable assumption). However, not every sequence is legal, only those in which every 1 has 0s for neighbors. How many sequences is that? An n-digit sequence has at most ⌈n/2⌉ 1s because otherwise there wouldn't be enough 0s to separate adjacent 1s (the last digit in the sequence must be 0 because otherwise there would be three adjacent 1s). * What is the mean number of hops made by a packet sent by S? The mean (expected) number of hops is the number of hops i times the probability that it takes i hops to go from S to D. For i less than 2, the probability is 0. For i = 2, the probability is (1 - p) sup 2, assuming each router makes its drop-no drop decision independently (which is an arguable assumption, but good enough for this problem).
The answers, approximately verbatim, and in no particular order:
-
Hops are number of routers/gateways a packet passes through to get from one
computer to another.
In computer networking, a hop represents one portion of the path between
source and destination. When communicating over the Internet, for example,
data passes through a number of intermediate devices (like routers) rather
than flowing directly over a single wire. Each such device causes data to
"hop" between one point-to-point network connection and
another. (computernetworking.about.com)
Based on that:
Hops made by a packet sent by it(S) are 3 hops.
Times a packet is sent by S:
In regular cases, a packet is sent from it(S) to it(D) once, so initial time
= 1.
it(S) keeps sending packet to it(D) as long as it(D) is not replying. That
means the times of retransmission depend on having replies from it(D) or not.
If it(S) received a reply, times of retransmission would be 0.
If it(S) didn't receive a reply, times of retransmission would be: n - 1.
Where n is the number of sent packets.
Hops made by a packet received by it(D) are 3 hops.
-
- First hop probability is p. for second hop probability is p(1 - p). For third hop it is (1 - p)(1 - p). So1 p + 2 x (1 - p)p + 3(1 - p)(1 - p) = p + 2p - 2p^2 + 3(1 - p) - p + p^2) = p + 2p - 2p^2 + 3(p^2 - 2p + 1) = p + 2p - 2p^2 + 3p^2 - 6p + 3 = p^2 - 3p + 3
- Probability of successful transmission is (1 - p)^2. The average number of transmission per packet is approximately 1/(1 - p)^2.
- average hops per packet = average hops per transmission x average no. of transmissions = (p^2 - 3p + 3)/(1 - p)^2
1: What happens if it takes more than three hops?
-
* Each packet may make 1, 2, or 3 hops. For 1 hop, the first router drops it
and the probability is p. For 2 hops, it goes through first router but not
the second and the probability is (1 - p)p. For 3 hops, it goes through
both routers and the probability is (1 - p)(1 - p). Average number of hops
made by a packet sent by it(S) is given by
1 x p + 2 x (1 - p)p + 3 x (1 - p)(1 - p)
= p + 2p - 2p^2 + 3 - 6p + 3p^2
= p^2 - 3p + 3
* The probability of successful transmission all the way is (1 - p)^2. Let
us denote it by w. The average number of times a packet is sent is given
by
w + 2w(1 - w) + 3w(1 - w)^2 + \(cdots\) nw(1 - w)^(n - 1) + \(\cdots\)
= 1/2w
= 1/(1 - p)^2
* Average number of hops made by a packet received by it(D) = Average hops made
by a packet sent by it(S) x Average number of times a packet is sent
transmissions is (p^2 - 3p + 3)/((1 - p) x (1 - p))
References: textbooks.
-
If host it(S) sends a packet to host it(D) and doesn't get a reply from it(D) within some
time, it resends the packet, and keeps resending the packet until it gets a
reply. it(D) only sends packets to it(S) in reply to packets received from S; D
never spontaneously resends a packet to S. Counting each network transit has
a hop, what is the average (mean) number of
* Hops made by a packet sent by S?
3 (once through N1 to G1, once through N2 to G2, and once through N3 to
D).2
* Times a packet is sent (initial + retransmissions) by S?
Assuming both G1 and G2 drop the packet on the first time 5 times.
* Hops made by a packet received by D?
Assuming G1 and G2 do not drop the packet at all 3 hops; if G1 drops the
packet and G2 does not then 4 hops. If both G1 and G2 drop the packet the
first time then 5 hops.
2: Does the packet ever get dropped?
-
- Hops made by a packet sent by S?
Each packet makes 1, 2, or 3 hops.
For 1 hop, the probability is p.
For 2 hops, the probability is (1 - p)p.
For 3 hops, the probability is (1 - p)(1 - p) = (1 - p)2.
The mean hops per transmission is3
(1 x p) + 2 x p(1 - p) + 3(1 - p)2) = p + 2(p - p2) + 3(p2 - 2p + 1) = p + 2p - 2p2 + 3p2 - 6p + 3 = p2 -3p + 3
x + 2x + (1 - x) + 3 times (1 - x)^2 + \(\cdots\) + n times (1 - x)^(x - 1) + \(\cdots\)
which will reduce to 1/x. Hence i.e.1/x = 1/(1 - p)^2
- Hops made by a packet sent by S?
Each packet makes 1, 2, or 3 hops.
For 1 hop, the probability is p.
For 2 hops, the probability is (1 - p)p.
For 3 hops, the probability is (1 - p)(1 - p) = (1 - p)2.
The mean hops per transmission is3
- Hops made by a packet received by b is
then the hops made by a packet received by is (p^2 - 3p + 3)/(1 - p)^2.mean hops = mean hops made by a packet sent by S * mean number of transmissions = (p^2 - 3p + 3) times (1/(1 - p)^2) = (p^2 - 3p + 3)/(1 - p)^2 3: But what happens if the packet is dropped?
-
Since there are three networks with two gateways in between them, assume it
takes two successful hops to reach it(D) from it(S) (one from N sub 1 to N sub 2 and
one from N sub 2 and N sub 3) and two successful hops to reach it(S) from D
(reverse order). Since p is the probability of a successful transfer from S
to it(D) or from it(D) to S. Let h equal the number of hops allowed before a packet
is dropped or lost.
1 The mean number of hops from it(S) to it(D) is equal to h*(1 - p) sup 2 such that
the mean is greater than or equal to 2. It takes a minimum of two hops to
reach it(D) from S. The formula described above is the total number of
possible hops multiplied by the probability of a successful transfer from S
to D.
1 The mean number of times a packet is sent from S is equal to h(1 - p)
sup 4 such that the mean is greater than or equal to 4. It takes at least
two hops to reach D from it(S) and another two hops fro the receipt packet
to reach it(S) from D. The formula described above is the total number of
possible hops multiplied by the probability of both a successful transfer
from it(S) to it(D) and a successful transfer from it(D) to it(S) (the receipt).
1 If the homework question is correct, then it appears to be the same as part
1 of this question. A packet that is received by it(D) will always be a packet
that was sent by it(S) in this scenario. If it is an error, the assumption is
that the question is looking for the mean number of hops made by a packet
sent by D. The only time it(D) will “resend” a packet is if it(S) does not
receive D's receipt packet, resends the initial packet for which the
receipt packet was sent, it(D) receives this packet (again), and it(D) sends another
receipt (the assumption being that the new receipt counts as a resend of
the original receipt message sent from D). the probability then remains
the same as part 1 anyway since it still takes two successive successful
hops to reach it(S) from D; therefore, the probability would be h*(1 - p)
2.
Source: Statistics Course at SJU during undergrad.
-
* Hops made by a packet sent by S?
A hop accrued each time that packets are passed to next router or gateway.
So, there are 2 gateways (2Gs), also if each network transit has a hop, so;
there are 3 networks (3Nets). Then, the average of numbers of hops made by
a packet sent by it(S) is 2 + 3 = 5 hops.
* Times a packet is sent (initial + retransmissions) by S?
it(S) will send a packet only one time is an initial, and it keeps
retransmitting (n) times until it(D) gets that packet. Then it(S) will stop
retransmitting to D. The average of numbers of times for a packet sent to
it(D) by it(S) is = (initial) time * (n) times of retransmissions.
* Hops made by a packet received by D?
There are 2 gateways. Also, if each network transit has a hop, so, there
are 3 networks. Then the average of numbers of hops made by a packet sent
to it(D) is 2 + 3 = 5 hops.
Reference is (www.en.wikipedia.org, Hop Count)
The difficulty with NACKs is they don't (shouldn't) occur often, and they don't mean much when they do occur. To provide a useful protocol, the receiver should NACK in such a way as to provide extra information. The sender can pipeline by sending packets in sequence at a regular interval. The usual reliability concerns can be dealt with using sequence numbers and time-outs. Because the problem's concerned with reliability and not efficiency, we can assume the transmission interval gets set and maintained using some mechanism, probably based on NACK arrival rates. The first problem is buffering at the sender. In the absence of other information, the sender has to buffer all the data sent because the receiver can NACK any packet. If the receiver adheres to the rule that it only NACKs the earliest (lowest sequence number) missing packet, then the sender can assume on receiving NACK i that all packets before i have been received. Although workable, this solution is not perfect because if the receiver never NACKs packets, the sender never clears the buffer. When the sender receives a NACK, it schedules a retransmission for the missing packet. In the presence of heavy packet loss, the protocol degenerates into stop-and-wait. Depending on packet-loss behavior, it might be useful to change NACKs to start plus run so groups of missing packets can be retransmitted on one NACK, but that's for efficiency, not reliability. The other problem is ending the transmission. Transmission end can be handled with NACKs (more or less) by having the sender end with an end-of-transmission (eot) packet. When the receiver gets an eot packet with sequence number i, it NACKs packet i + 1. When the sender gets NACK i + 1, it knows the receiver has all the data, and the transmission is at an end. The protocol response to lost packets depends entirely on rate at which NACKs arrive at the sender, it has nothing to do with the rate at which the sender receives data to send.
The answers, approximately verbatim, and in no particular order:
-
Since the protocol will only implement NACKs (negative acknowledgments), it
will send packets into the pipeline until the receiver is nearly pushed to
its capacity (as discussed in class 10/02/2012). It will then wait for an
allotted amount of time (a grace period) before it continues to send packets
into the pipeline. This allocated time is used to obtain and handle NACKs
sent from the receiver should one of the packets not reach it (the receiver).
If the sender receives a NACK, it will resend the corresponding packet. This
system ensures reliability. This protocol will respond slowly if the arrival
rate of data to the sender is low because it will take more time to receive
the NACK and take the corresponding action; conversely, it will respond
quickly if the arrival rate is high since the receiver will quickly issue a
NACK that returns to the sender promptly within the retransmission time.
[ picture ]
-
The protocol response to the lost packet when the arrival [??] of the data to
the server is lost is also lost and the protocol[?] response is the lost
packet when[?] the arrival rate of the data to the sender is high is also
high i.e. it is quick because when a sender sends a packet to the receiver
and the packet is reached[?] then the receiver gets an acknowledgment and
sends another packet and when the sender sends a packet and the packet is
lost and the receiver sends a negative acknowledgment i.e. NACK the receiver
waits the packet is obtained and when it is got then the [??] starts[?].
Hence the response rate is [??] as the arrival rate of the data to the
sender.1
1: What does this paragraph say? Is there a protocol described in here?
-
In a protocol that using only negative acknowledgments, the loss of packets
is only detected by the receiver when it receives it(x) - 1 and then it(x) +
1, only when it(x) + 1 is received makes the receiver realize that it(x) was
lost. When the arrival rate of data to the sender is low then there will be
a delay in receiving NAKs for lost packets by the sender. So, there will be
a delay in sender's response, i.e., delay in retransmission. If there is a
long delay between the transmission of it(x) and the transmission of it(x) +
1, then it will be a long time until it(x) can be recovered, under a NACK only
protocol.
On the other hand, if arrival rate of data is high, then recovery under a
NACK-only protocol could happen quickly. Moreover, if errors are infrequent,
then NAKs are only occasionally sent (when needed), and ACKs are never sent,
a significant reduction in feedback in the NACK-only case over the AC-only
case.
Reference: \
Kurose and Ross textbook
-
With a reliable data pipelined data transfer protocol that uses only negative
acknowledgment it would take longer for the protocol to respond to lost
packets when the arrival rate is low. The lost of packet x is only
noticed by the receiver when packet x + 1 is received. However if data
is sent more frequently then recovery could happen quickly.2
2: What is the protocol being described?
-
As known, in the pipelined reliable data transfer protocol the sender can
start sending a second data packet before the sender receives the
acknowledgment for the first data packet.3 Thus, if the sender needs to send many
packets, then the time until the last of the packets is sent will be shorter
with a pipelined protocol. Also, errors can occur when a pipelined protocol
is used in two ways, which are losing or corrupting data and losing or
corrupting acknowledgments.
* The pipelined reliable data transfer protocol will respond to lost packets
by using the (Go Back N) which is the sender transmits ALL the data packets
it had sent since the lost or corrupted data packets because when the
arrival rate of data to the sender is low, that means there is much lost or
corrupted data packets. Thus, there is a need to retransmits all lost or
corrupted data packets to save time.
[ picture ]
* The same idea for lost or corrupted ACKs.4
* The pipelined reliable data transfer protocol will respond to lost packets
by using the (Selective Repeat) which is the sender JUST retransmits the
lost or corrupted data packet because when the arrival rate of data to the
sender is high, that means there is not much lost or corrupted data
packets. Thus, there is no need to retransmits all lost or corrupted data
packets to save time.
[ picture ]
* The same idea for lost or corrupted ACKs.
Reference is (Computer Networking a Top Down Approach, pages 203--211).
3: Is that pipelining, or using negative acknowledgments?
4: How are lost acks, or NACKs, detected?
-
A pipelined data transfer protocols is based on the idea of sending multiple
packets by the sender without waiting for acknowledgment after each packet.
Instead, the sender is allowed to send number of packets before waiting for
an acknowledgment. As a result, the range of sequence numbers must be
increased and packets have to be buffered at least at the sender side. A
sample of pipelined transfer protocol is presented in figure 1.
Pipelined protocol provides reliability which means that there is no loss in
data, corrupted data, or unordered data.
(Kurose and Ross. Computer Network: A Top-Down Approach. Fifth edition)
[ picture ]
Steps of designing a pipelined data transfer protocol and they would be
integrated with Figure 1.
Version 1
Sender: [ picture ] packet = make(data) & send(packet)
Receiver: [ picture ] data = extract(packet) & deliver(data)
Version 2: Acknowledgment
We implement techniques like checksum to ensure that the data were
transmitted without error by comparing the umber of bits that were received
by the receiver with the numb er of bits that were sent by the sender.
Sender: [ picture ]
If NACK? \
Send again
Receiver: [ picture ]
If packet is received & checksum = True \
Then, Extract data & deliver data & send ACK
Pipelined protocol deals with lost packet with two approaches:
1 Go-Back_N
1 Selective Repeat
In Go-Back-N approach, the sender sends packets up to the lost packet again
to the receiver. This makes the network suffers of performance problem when
the network is slow.
In selective repeat, the sender sends specific packets that were lost or
corrupted. This reduces redundancy and fasts the data transform rate.
When we have slow arrival rate of data, it is better to apply selective repeat
approach to avoid overwhelming the network. Otherwise, using Go-Back-N is
not a problem when we have fast data arrival.
-
In this type of protocol,5 if the receiver doesn't receive the packet from sender, it sends
a NACK, and when the sender receives it, it sends a new packet.6
If the arrival of NACK is slow the sender waits until it receives it. So
when it is low, the protocol response is also low.
When it is high, the sender also responds quickly.
5: What type of protocol? Where is it described?
6: A new packet? What about the packet that wasn't received?