Intelligent Systems Lecture Notes

25 November 2011 • Reinforcement Learning

---

Outline

• Markov decision processes.
• Reinforcement learning.
  • Passive reinforcement learning.
    • Direct utility estimation.
    • Active dynamic programming.
    • Temporal-difference learning.

Markov Decision Processes

• S = { 11 12 13 21 23 31 32 33 41 42 43 }.
• A = { l r u d }.

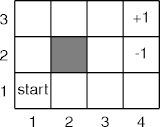
  S' 11 12 21 13 ··· A u u u u ··· S 11 11 11 11 ··· Pr(S' | S, A) 0.2 0.7 0.1 0 ··· S' 43 33 23 32 ··· A r r r r ··· S 33 33 33 33 ··· R(S, A, S') 1 -0.04 -0.04 -0.04 ···

Reinforcement Learning

• An agent works in a fully observable world.
• The agent uses a Markov decision process, but the agent doesn’t know
  • the transition function Pr(), and
  • the reward function R().
• The reinforcement learning problem determines an optimal policy, or close to it.

A Warm-Up Problem

• The agent has π. How can it find V^π?

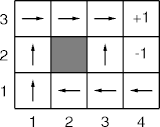
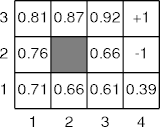
  π		Vπ

• The passive learning problem determines how good π is (or, it finds V^π using π).

Passive Learning

• The general idea is to run experiments, record the results, and analyze the history.
• A trial is a sequence of state, action, reward triples
  • s₀, a₀, r₀, s₁, a₁, r₁, …
  • s₀ is the initial state; the last state s_k is a terminal state.
• Assume the discount rate is γ = 1.

Estimating V^π()

• Given a trial of k steps

  s₀, a₀, r₀, …, s_i, a_i, r_i, …, s_k, –, r_k

• estimate the utility of s_i as the sum of the rewards from steps i through k.
• V^π(s_i) is the mean of all sums for s_i for all trials.
• This is known as direct utility estimation.

Example

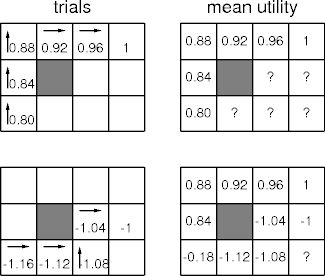
Observations

• Direct utility estimation doesn’t know about the stochastic relation among squares.

  

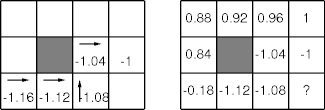
  • The mean utility for 31 should leach off 10% of the mean utility for 33.
• Direct utility estimation can converge slowly.

Improving DUE

• To improve on direct utility estimation, estimate the transition function Pr() too.
• Once Pr() is known, everything in in the right-hand side of

  Q^π(s, a) = \(\sum\)_n Pr(n | s, a)(R(s, a, n) + γV^π(n))

• has been estimated, providing an estimate for Q^π().
  • And Q^π() leads to V^π().

Estimating Pr()

• Counts taken from trials estimate the transition conditional probabilities.
• Given

  …, 11, up, 12, …
  …, 11, up, 21, …
  …, 11, up, 12, …
  

• then

  Pr(12 | 11, up, 11) = 2/3
  Pr(21 | 11, up, 11) = 1/3

Finding V^π()

• Once Q^π() is in hand, V^π() can be found by solving the related linear-equation set.
• Alternatively, the estimates can be created iteratively using adaptive dynamic programming (ADP).
  • Adaptive dynamic programming provides continuous results (of varying quality), and fast convergence.
• Adaptive dynamic programming is a variant of MDP policy iteration.

ADP Algorithm

passive ADP(sn, rn)
	if V[sn] = null then V[sn] = R[sn] = rn
	if sc ≠ null
		Nsa[sc, ac]++
		Nssa[sn, sc, ac]++
		for each s ∈ S do
			Pr[s, sc, ac] ← Nssa[s, sc, ac]/Nsa[sc, ac]
	V ← the solution to the related linear equations
	if sn is terminal
	then sc, ac ← null
	else sc, ac ← sn, π[sn]
	return ac

Further Improvements

• After picking up V^π() and Pr() from the traces, is there anything left top pick up?
  • And if so, how can we exploit it to get better results?
• DUE and ADP compute means.
  • More importantly, mean computations over related, and improving, data.
• What can you do with means?
  • But first, what’s wrong with them?

Mean Problems

• The straightforward mean calculation

  (v₁ + \(\cdots\) + v_n)/n

  treats (weights) all values the same.
• As an algorithm converges, later values are better (more accurate) than earlier values.
• A better mean would weight later values over earlier values.

Computing Averages

• Let Ak be the average of k samples
  	Ak	=	(v1 + \(\cdots\) + vk)/k
  Multiply by k
  	kAk	=	v1 + \(\cdots\) + vk - 1 + vk
  		=	(k - 1)Ak - 1 + vk
  Divide by k
  	Ak	=	(1 - 1/k)Ak - 1 + vk/k
  Let αk = 1/k
  	Ak	=	(1 - αk)Ak - 1 + αkvk
  		=	Ak - 1 + αk(vk - Ak - 1)

The Temporal-Difference Error

• Rewriting (v₁ + \(\cdots\) + v_k)/k as

  A_{k - 1} + α_k(v_k - A_{k - 1})

• emphasizes two values:
  • v_k - A_{k - 1}, the temporal-difference error,
  • α_k, the learning rate.
• The learning rate is a knob controlling the value of the present (away from 0) over the past (near 0).

Learning Rate

• The learning rate α_k = 1/k is a function of k.
  • New values add decreasingly smaller amounts to the average.
  • Converges to the mean, doesn’t exploit more accurate or representative values.
• A constant learning rate α ∈ (0, 1]
  • Favors new values over the average.
  • Responds to change, but doesn’t converge to the mean.

Learning-Rate Example

Move the mouse pointer over the lighter curves at the data points (bends in the curve) to highlight the curve.

The Q-Learning Algorithm

Q-learning(S, A, γ, α)
	Q[s, a] ← whatever
	s ← start state
	repeat
		pick a from A and perform it in state s
		observe the reward r and next state n
		Q[s, a] ← Q[s, a] + α(r + γmaxan Q[n, an] - Q[s, a])
		s ← n
	until done

Summary

• Reinforcement learning recovers information from a partial Markov decision process.
• Passive reinforcement learning judges policy from execution histories.
• When life gives you lemons, take the mean.
  • Possibly using temporal differences.

References

• Reinforcement Learning (Chapter 21) in Artifical Intelligence, third edition, by Stuart Russell and Peter Norvig, Prentice Hall, 2010.