A decision tree fails when it can't use the input-feature values to predict the target feature values, which occurs when the input features don't distinguish among the target features.
One possibility is to define a set of n spam words, and then set up an n+1 dimensional space. The first n dimensions, one per spam word, are binary valued and indicate whether or not the associated spam word appears in the message. The last dimension is also binary valued and indicates whether or not the message is spam.
Alternatively, and even simpler, set up a 2-dimensional space. The x axis indicates the total number of spam words appearing in a message, and the y axis is binary valued and determines whether or not the message is spam.There would be no difference. The problem with direct utility estimation is that it assumes the actions are deterministic, and fails to account for any bleed-over into a state resulting from actions other than the intended action.
It is not possible. Suppose the sum-of-squares error dropped significantly for k, but remained more or less the same for k - 1 and k - 2.
Define the point estimator to be 42. The maximum error is
Pr(C) represents the classification prediction; it is also needed to compute Bayes' rule.
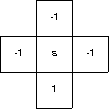
A Q-learning agent operates in the world shown to the right. The start state is marked “s”; the remaining states are terminal states. The agent can move up, down, left, or right with a 50% probability of success; that is, half the time the agent moves as directed, and half the time the agent doesn't move. The reward for reaching a terminal state is given in the state; the reward for staying at the start state is 0.
Describe the entries in the Q array discovered by the agent.
There are five states and four actions, so the Q array is a 5×4 table. Four of the states are terminal, so any action in those states are ignored, and there are no more policy moves from them. Assuming there is no reward for staying in the terminal state, the expected utility of those 4×4 states is 0.
The last state is the start state. There is a 0.5 probability a down action will be successful; if it is, the utility is 1 and if it isn't the utility is 0. The expected utility is then 0.5(1) + 0.5(0) = 0.5. If the action fails, there's a 0.5 probability the next one will be successful. Assuming independence between moves (a dodgy assumption, but a simplifying one), the expected utility is the sum of the expected utilities of the individual moves, leading to a 0.5 expected utility overall. A similar argument holds for the other moves from the start state, except the reward in those cases is -1, and the expected utility is -0.5.If alpha is greater than 1, then there is a tendency to overcompensate for errors, which makes it difficult to converge to the mean, and be driven into instability when reacting to changes.