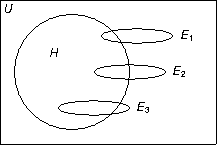
write the formula for the conditional probability of H given a single observation Ei as evidence. The conditional probability you give should be the largest among all conditional probabilities for H given a single observation. Using the Venn diagram as a guide, estimate the probability of your formula. Justify your answers.
The conditional-probability formula for h given the observation ei is Pr(h | ei) = Pr(h \(\cap\) ei)/Pr(ei) for i = 1, 2, or 3. Assuming a uniform distribution of outcomes in the universe U, the Venn diagram suggests the observations ei are all the same size, which makes Pr(ei) the same for i = 1, 2, and 3.
With the denominators the same, the largest ratio Pr(h | ei) will have the largest numerator. The Venn diagram makes clear Pr(h | e3) is larger than the other two conditional probabilities. Estimating the overlap between h and e3 puts Pr(h | e3) somewhere in the range 0.8 to 0.9.
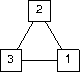
Each room can hold a coconut or a lime, but not both, or it holds nothing. The agent can carry a coconut or a lime, but not both, or it carries nothing. The agent is always in one of the three rooms. Describe the features needed to represent this world.
A straightforward translation of the problem gives
A somewhat less straightforward translation of the problem gives
Feature Domain ALOC { 1, 2, 3 } AHAS { lime, coconut, nothing } 1HAS { lime, coconut, nothing } 2HAS { lime, coconut, nothing } 3HAS { lime, coconut, nothing }
where \(\mathcal{P}\)(S) is the powerset of S. The problem statement is silent on the possibility of a room having more than one lime or coconut. A problem for which cardinally is important might use the feature set
Feature Domain ALOC { 1, 2, 3 } COCONUTHOLDER \(\mathcal P\)({ 1, 2, 3, A }) LIMEHOLDER \(\mathcal P\)({ 1, 2, 3, A })
where y is { 1, 2, 3 } and x is y \(\cup\) { A }.
Feature Domain COCONUTSINx \(\mathbb{N}\) LIMESINx \(\mathbb{N}\) AGENTSINy \(\mathbb{N}\)
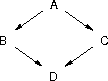
Define the rest of the belief network using the DAG as your guide.
A belief network is defined in three parts. The first part defines the random variables and their domain. From the network diagram, the random variables are A, B, C, and D. The binary domain is the simplest for the random variables; other domains are possible but entail more work in the third part than does the binary domain.
The second part of the belief-network definition is the conditional-independence relation among the random variables. These relations were given by the DAG in the problem statement.The third part is the conditional-probability distributions over the random variables. Subject to the probability axioms, the distributions are arbitrary; for example
Pr(a) pa Pr(\(\neg\) a) 1 - pa Pr(b | a) 0.1 Pr(b | \(\neg\)a) 0.2 Pr(c | a) 0.4 Pr(c | \(\neg\)a) 0.5 Pr(d | b \(\wedge\) c) 0.1 Pr(d | \(\neg\)b \(\wedge\) c) 0.2 Pr(d | b \(\wedge\) \(\neg\)c) 0.3 Pr(d | \(\neg\)b \(\wedge\) \(\neg\)c) 0.4
- mcc: move to the room counter-clockwise adjacent to the room containing the agent.
- mc: move into the room clockwise adjacent to the room containing the agent.
- exch: the agent puts down whatever it’s carrying (if anything) and picks up whatever the room holds (if anything).
mc ; exch ; mc ; exchwould be represented using delta encoding. Justify your answer.
Let a state in the state-space representation be the five tuple (ALOC, AHAS, 1HAS, 2HAS, 3HAS). Assume the lower-case version of a feature name represents a value from the feature’s domain. Starting from the given state, the delta representation of the actions are
(ALOC = 1, AHAS = n, 1HAS = n, 2HAS = l, 3HAS = c) mc { ALOC = 3 } exch { AHS = c, 3HAS = n } mc { ALOC = 2 } exch { AHS = l, 3HAS = c }
From the answer to question 3, the conditional probabilities for B are
To get B’s unconditional probability, sum-out A:
Pr(b | a) 0.1 Pr(b | \(\neg\)a) 0.2
Pr(b) = \(\sum\)a \(\in\) dom(A) Pr(b | a) = Pr(b | true) + Pr(b | false) = 0.1 + 0.2 = 0.3
The agent is in room 1, which is otherwise empty. Room 2 has a coconut. Room 3 has a lime. The agent isn’t carrying anything.The goal state of triangle world is
Room 1 has a coconut, room 2 is empty, and room 3 has a lime. It doesn’t matter where the agent is or what it’s carrying.Assuming your world description given as the answer to question 2 and a STRIPS representation of the agent actions given in question 4, show the sequence of actions regression planning might generate to achieve the goal state from the current state. Don’t show the full derivation, just the path between current and goal states. Justify the steps in the derivation.
The regression planning’s goal state G is the
problem’s initial state: G: (1HAS = n, 2HAS = c, 3HAS = l)Because the problem goal state doesn’t care about the agent, those features are omitted. The initial state in regression planning is the problem’s goal state. |
|
| (1HAS = c, 2HAS = n, 3HAS = l) | |
| If we assume the agent’s in room 1 and holding a coconut,
then an exch action will produce the initial state, and set 1HAS
equal to its value in the goal state. \(\downarrow\) exch |
|
| (ALOC = 1, AHAS = c, 1HAS = n, 2HAS = n, 3HAS = l) | |
| Moving the agent counter-clockwise from room 1 puts it in room 2.
mcc doesn’t change the current state’s relation to
the goal state, but it sets up the next action. \(\downarrow\) mcc |
|
| (ALOC = 2, AHAS = c, 1HAS = n, 2HAS = n, 3HAS = l) | |
| A final exch between the agent and room 2 makes the goal
state a subset of the current state, ending the search. \(\downarrow\) exch |
|
| (ALOC = 2, AHAS = n, 1HAS = n, 2HAS = c, 3HAS = l) | |
If a belief network is a tree, then it’s a Markov chain because each random variable is directly conditioned by at most one other random variable.
Assume the five-tuple world representation (ALOC, AHAS, 1HAS, 2HAS, 3HAS). The agent location ALOC is effected by the mc action and uneffected by the exch action.
None of the having features are effected by the mc action,
ALOC\('\) = x \(\leftarrow\) ALOC = x \(\wedge\) Act = exch ALOC\('\) = x \(\leftarrow\) ALOC = y \(\wedge\) x = ((y - 1) mod 3) + 1 \(\wedge\) Act = mc
but all having features are effected by the exch action
iHAS\('\) = x \(\leftarrow\) iHAS = x \(\wedge\) i \(\in\) { 1, 2, 3, A } \(\wedge\) Act = mc
iHAS\('\) = x \(\leftarrow\) iHAS = y \(\wedge\) AHAS = x \(\wedge\) i \(\in\) { 1, 2, 3 } \(\wedge\) Act = exch AHAS\('\) = x \(\leftarrow\) AHAS = y \(\wedge\) iHAS = x \(\wedge\) i \(\in\) { 1, 2, 3 } \(\wedge\) Act = exch