Intelligent Systems Lecture Notes

23 November 2011 • Markov Decision Processes

---

Outline

• An agent’s world.
• Markov decision processes.
• Policy values.
• Optimal policy values.
• Computing optimal policies.
  • Iterating over values.
  • Iterating over policies.

Agent’s World

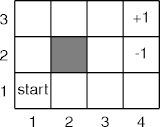
An agent acts until it reaches a goal state (4, 3) or (4, 2). The agent accrues utility with each action.

• The objective is to accrue maximum utility.
• An agent can fully observe the world.

Agent’s Actions

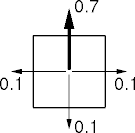
An agent can move up, down, left, and right one square. With a 0.3 probability of failure.

• An agent bumps in to an obstacle and remains in place.
  • The world is surrounded by a wall.

Agent’s Utility

Goal (4, 3) adds 1 to the utility (a reward). Goal (4, 2) subtracts 1 from the utility (a penalty or punishment).

• Non-goal states have a 0.04 penalty.

Agent’s Problem

• How should the agent accrue maximum utility?
• A simple planning problem, except for stochastic behavior.
• The agent follows a stationary policy (or just policy) π : S → A to determine its behavior.
  • How does the agent formulate a policy?
  • How does the agent formulate an optimal policy π^*?

Markov Decision Processes

• The problem can be modeled as a Markov decision process (MDP):
  • A set S of world states.
  • A set A of actions.
  • A probability function Pr : S × S × A → [0, 1] such that

    ∀ s ∈ S, ∀ a ∈ A \(\sum\)_{s\('\) ∈ S} Pr(s\('\) | s, a) = 1

  • A reward function R : S × A × S → \(\mathbb{R}\).

MDP Illustrated

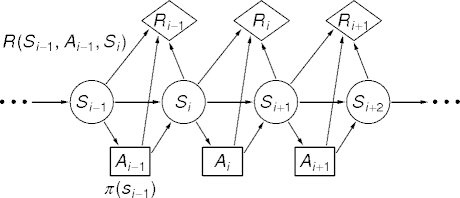
MDP Example

• S = { 11 12 13 21 23 31 32 33 41 42 43 }.
• A = { l r u d }.

  S' 11 12 21 13 ··· A u u u u ··· S 11 11 11 11 ··· Pr(S' | S, A) 0.2 0.7 0.1 0 ··· S' 43 33 23 32 ··· A r r r r ··· S 33 33 33 33 ··· R(S, A, S') 1 -0.04 -0.04 -0.04 ···

Reward History

• In addition to world state, the agent can keep a rewards history (cumulative reward, value, or utility) r₀, r₁, …
• The discounted reward V is a summary of a rewards history

  V = r₀ + γr₁ + γ²r₂ + \(\cdots\) = \(\sum\)^∞ γⁱr_i

• for the discount rate γ ∈ [0, 1].
  • γ a preference for immediate (near 0) over long term (near 1) gain.

Valuing Policy

• There are lots of policies. How does one policy compare to another?
  • And so, what’s the best policy?
• V^π(s) is the expected value of following policy π in state s.
• For algorithmic reasons, define Q^π(s, a) as the expected value of
  • doing action a in state s, then
  • following policy π.

V^π() and Q^π()

• The functions V^π() and Q^π() are related:

  Qπ(s, a)	=	\(\sum\)s' Pr(s' | s, a)(R(s, a, s') + γVπ(s'))
  Vπ(s)	=	Qπ(s, π(s))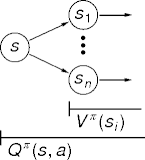

  

Optimal Policy Values

• Q^*() is the expected value of doing action a in state s and then following the optimal policy:

  Q^*(s, a) = \(\sum\)_s' Pr(s' | s, a)(R(s, a, s') + γV^*(s'))

• V^*() is the expected value of following the optimal policy in state s:

  V^*(s) = max_a Q^*(s, a)

Optimal Policies

• Given Q^*() and V^*(), the optimal policy π^*() is defined as

  π^*(s) = a | ∀ a\('\) ∈ A : Q^*(s, a) ≥ Q^*(s, a\('\))

Value-Iterations Algorithm

value iteration(S, A, Pr, R, θ)
	V0[*] ← 0
	k ← 0
	repeat
		k++
		for each s ∈ S do
			Vk[s] ← maxa \(\sum\)n Pr(n | s, a)(R(s, a, n) + γVk - 1[n])
	until ∀s |Vk[s] - Vk - 1[s]| < θ
	for each s ∈ S do
		π[s] ← a maximizing \(\sum\)n Pr(n | s, a)(R(s, a, n) + γVk[n])
	return π, Vk

Computing V^π() Without Q^π()

• Given a policy π, what is V^π()?
  • From the definition, V^π(s) = Q^π(s, π(s)).
• V^π() can be rewritten as a set of n linear equations in n unknowns, n = |S|.

  0	=	c10 + c11Vπ(s1) + \(\cdots\) + c1nVπ(sn)
  	\(\vdots\)
  0	=	cn0 + cn1Vπ(s1) + \(\cdots\) + cnnVπ(sn)

Improving π

• If π isn’t optimal, there’s a policy π\('\), action a, and state s such that Q^π(s, a) < Q^π\('\)(s, a).
  1. Solve linear equations defined by V^π().
  2. For each s and a, compare V^π(s) to Q^π(s, a).
     • If V^π(s) < Q^π(s, a), then π(s) makes the wrong choice, and should be set to a.
  3. Iterate steps 1 and 2 until stable.

Policy-Iterations Algorithm

policy iteration(S, A, Pr, R)
	π[*] ← whatever
	repeat
		unchanged ← true
		V ← the solution to the linear equations given by π
		for each s ∈ S do
			Qbest ← V[s]
			for each a ∈ A do
				Qsa ← \(\sum\)n Pr(n | s, a)(R(s, a, n) + γV[n])
				if Qsa > Qbest
					π[s] ← a
					Qbest ← Qsa
					unchanged ← false
	until unchanged
	return π

Summary

• A Markov decision process handles stochastic model behavior.
  • Discover a good policy for achieving goals.
• Incremental algorithms handle infinite systems by quitting early.
  • When results are good enough.
• Value iteration finds better policies by construction.
• Policy iteration finds better policies by comparison.

References

• Making Complex Decisions (Chapter 17) in Artifical Intelligence, third edition, by Stuart Russell and Peter Norvig, Prentice Hall, 2010.