Intelligent Systems Lecture Notes

12 October 2011 • Basic Planning

---

Outline

• Forward planning.
• Regression planning.

Planning

• Given a description of
  • the effects and preconditions of agent actions,
  • the initial world state,
  • the goal state to achieve,
• find a sequence of actions that results in a state satisfying the goal.

Planning Goals

• A planning goal is a subset of features from the world model, each with a specific value.
  • Goal G = { f₁ = v₁, f₂ = v₂, … }
  • Goal.features \(\subseteq\) World.features.
• A world state w satisfies a goal g if g is a subset of w.
  • g \(\subseteq\) w
  • This includes features and values.

Forward Planning

• Haven't we solved this problem?
  • Yes, we have.
• Search the state-space graph.
  • Vertices represent the states.
  • The edges from state s represent legal actions in state s.
• A plan is a path from the initial state to a state satisfying the goal.

Example

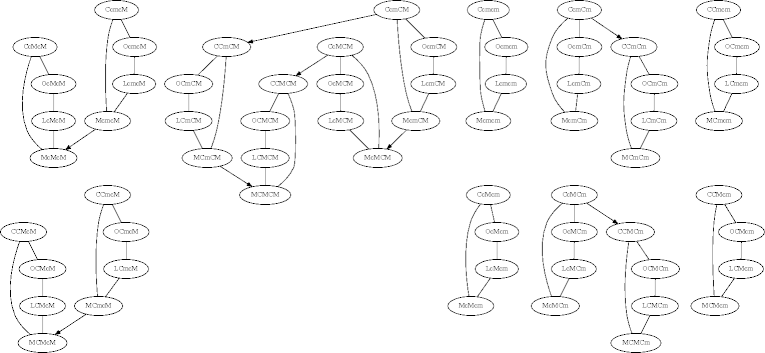
State-Space Vertices

• Each vertex in the state-space graph is a snapshot of the world.
  • Vertex size is linear in world-feature count, which may be in the 100s.
  • Vertex count grows exponentially with feature cardinality.
• How can these sizes be tamed?
• Important observation: adjacent vertices usually differ in a small number of features.
  • Why?

Delta Encoding

• Use delta encoding to represent a sequence of large objects differing from each other by small amounts.

  LO₁, LO₂, LO₃, …
  LO₁, (LO₂ - LO₁), (LO₃ - LO₂), …

  • An old engineering trick (PCM, CVS).
• For state-space vertices, the differences are feature changes.

Delta-Encoding Example

• There's the benefit; what's the cost?

Observations

• Dealing with the whole world requires a possibly long, but usually simple, calculation.
  • Goal detection.
  • Are two worlds the same (cycle detection)?
  • Fortunately, delta encodings are themselves highly compressible.
• The search graph is constructed on demand, and only the reachable states.

Improving Search Efficiency

• Exploit domain knowledge to improve search efficiency.
  • Use heuristics to improve choices.
    • Compare the costs of moving clockwise and counter-clockwise to reach loc.
  • Prune neighbors using domain knowledge.
    • Just moved from X from Y? Don't move back to Y next.

Regression Planning

• Idea: search backwards from the goal description: vertices correspond to subgoals, and edges to actions.
  • Nodes are propositions: a formula made up of assignments of values to features.
  • Edges correspond to actions that can achieve one of the goals.
  • Neighbors of a vertex v associated with edge e specify what must be true immediately before e so that v is true immediately after.
  • The start node is the goal to be achieved.
  • goal(v) is true if v is a proposition that is true of the initial state.

Vertices and Edges

• Represent a vertex v as a set of value-variable assignments:

  [ X₁ = v₁, …, X_n = v_n ]

  These are the assignments you want to hold.
• The last action achieves X_i = v_i and does not achieve X_j = v_j' where v_j' is different from v_j.
• The neighbor of v along edge e must contain:
  • The action A prerequisites.
  • The elements of v not achieved by A.
  v must be consistent.

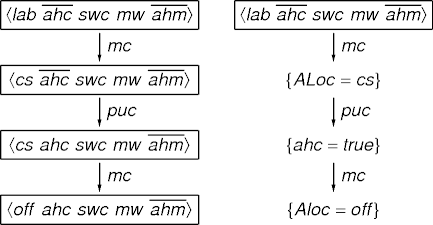
STRIPS Example

• \(\langle\)G, A, N\(\rangle\) where G = [ X₁ = v₁, …, X_n = v_n ] is an arc if
  • X_i = v_i is an effect of action A for some i.
  • X_j = v_j' and v_j' \(\neq\) v_j is not an action A effect.
  • N is preconditions(A) \(\cup\) { X_k = v_k : X_k = v_k \(\not\in\) effects(A) } and N does not assign different values to any variable.

Regression Example

Find the Errors

Optimizations

• Goal G₁ is simpler than goal G₂ if G₁ is a subset of G₂.
  • It’s easier to solve [ cs ] than [ cs, ahc ].
• If you have a path to node N have already found a path to a simpler goal, you can prune the path N.

Improving Efficiency

• A heuristic function to estimate how difficult it is to solve the goal from the initial state.
• Domain-specific knowledge to remove impossible goals.
  • It is often not obvious from an action description to conclude that an agent can only hod one item at any time.

Forward vs Regression Planning

• Which is more efficient depends on
  • The branching factor.
  • How good the heuristics are.
• Forward planning is unconstrained by the goal (except as a source of heuristics).
• Regression planning is unconstrained by the initial state (except as a source of heuristics).

Summary

References

• Planning in IS (Chapter 12) in Intelligent Systems by Robert Schalkoff, Jones and Bartlett, 2011.
• Classical Planning (Chapter 10) in Artifical Intelligence, third edition, by Stuart Russell and Peter Norvig, Prentice Hall, 2010.
• Planning (Chapter 15) in Knowledge Representation and Reasoning by Ronald Brachman and Hector Levesque, Morgan Kaufmann, 2004.

---

This page last modified on 2011 October 9.