Intelligent Systems Lecture Notes

9 November 2011 • Basic Learning

---

Outline

• Basic learning models.
  • Decision trees.
  • Linear regression.
  • Bayesian classifying.

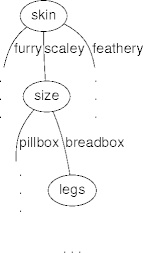
Let’s Play a Game

I am thinking of an animal.

What kind of skin does it have?

Furry

Is it around the size of a bread box?

Yes

And so on\(\ldots\)

• How would you teach a computer to play this game?

Game-Play Tree

This is the essence of a decision tree.

Decision Trees

• A decision tree for a target feature is an m-way tree with:
  • interior nodes labeled with input features.
  • edges labeled with values from the source-node input feature.
  • leaves labeled with point predictions for the target feature.

Decision Tree Examples

Trees to Rules

• In a deterministic decision tree each leaf node resolves to a target domain value.
  • Rather than a probability distribution.
• A deterministic decision tree can be turned into a propositional knowledge base.
  • Each leaf value is a rule head.
  • The conjunct of edge labels on the path from the root to the leaf is the rule body.
  • leafvalue \(\leftarrow\) edgelabel \(\wedge\) \(\cdots\) \(\wedge\) edgelabel

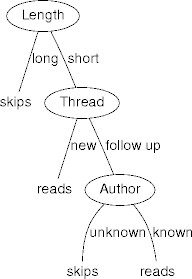
Tree KB Example

skips \(\leftarrow\) long reads \(\leftarrow\) short \(\wedge\) new skips \(\leftarrow\)   short \(\wedge\)   followup \(\wedge\)   unknown reads \(\leftarrow\)   short \(\wedge\)   followup \(\wedge\)   known

Selecting Decision Trees

• There are a huge number of decision trees for a given input set.
• A bias can order the candidate trees in decreasing fidelity to the bias.
  • The bias selects for low height trees, low node count trees, best predicting trees, …
• But how are decision trees generated?

Generating Decision Trees

• Given
  • an input-feature set \(I\) = { \(I\)₁, …, \(I\)_k },
  • a target feature T, and
  • a training-example set E = { \(\ldots\), (\(I\)₁, …, \(I\)_k, T) }.
• generate a decision tree.
• General idea: pick an input feature, recurse on each input-feature value v to create a subtree rooted at v.

Decision-Tree Generator

decision tree DTG(I, T, E)

  if stop here(E)
    return point estimate(T, E)

  I' = pick(I)
  root = node(I')
  for v in dom(I')
    root.add child(
      DTG(I, T, {e ∈ E | val(e, I') = v})

  return root

Observations

if stop here(E)
  return point estimate(T, E)

• There are many stopping criteria.
  • Identical target-feature values.
    • The point estimator returns the target-feature value.
  • The tree depth has maxed out.
    • The point estimator returns a probability distribution over the example target-feature values.

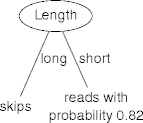
Stopping Examples.

• Stop with depth 1 trees, predict Action.
• Training examples:

  Action Author Thread e1 skips known new e2 reads unknown new e3 skips unknown old e4 skips known old e5 reads known new e6 skips known old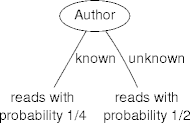

Stopping Examples..

• Stop with no decision needed, predict Action.
• Training examples:

  Action Author Thread e1 skips known new e2 reads unknown new e3 skips unknown old e4 skips known old e5 reads known new e6 skips known old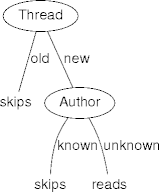

Observations

I' = pick(I)

• There are many ways to pick the next input feature.
  • The feature picked should most support the bias.
• Pick randomly, or with greed.
  • Greed optimizes exactly the next choice.
  • This is the myopically optimal choice.
• Chose large input features before smaller ones.
  • Trees have fewer nodes that way.

Using Decision Trees

• Given a decision Tree D and an input set \(I\), predict the target feature value.
• Basic idea: search the tree on the edge labels rather than the node labels.

target feature predict(D, I)
  if leaf(D)
    return D.label
  else
    return 
      predict(D.child[val(I, D.label)], I)

Linear Regression

• A linear function of features \(I\)₁, …, \(I\)_n is a function of the form

  f ^w(\(I\)₁, …, \(I\)_n) = w₀ + w₁\(I\)₁ + \(\cdots\) + w_n\(I\)_n = w₀ + \(\sum\)_j w_j\(I\)_j

• where

  w = (w₀, …, w_n)

• is the weight vector.

Linear Regression

• A linear regression is the output of a linear function of an input example e and weight vector w):

  pval w(e, T) =
  	w0 + w1val(e, \(I\)1) + \(\cdots\) + wnval(e, \(I\)n)

Weight Vector

• The weight vector is a set of knobs for minimizing error.
• Supposing a sum of squares error measure

  Error_E(w) = \(\sum\)_{e \(\in\) E}(val(e, T) - pval ^w(e, T))²

• find w to minimize Error_E(w).

Finding Weight Vectors

• Minimizing weight vectors can be computed analytically.
  • See any mathematical software system: Mathematica, R, SAS, \(\ldots\)
• There are regression techniques that can’t be handled analytically.
  • And error measures too.
• Need a more general approach than closed-form calculation.

Gradient Descent

• When you want to go down hill, step down the slope, not up.
• Gradient descent is the iterative calculation that steps down the slope.

  

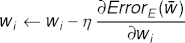
  • \(\eta\) is the learning rate, another knob.

Gradient Descent Code

weight vector GD(I, T, E, η)

  wvec = random initialization

  repeat
    for e in E
      δ = val(e, T) - pval(wvec, e, T)
      for i in wvec.size
        w[i] = w[i] + ηδval(e, I[i])
  until done

  return wvec

Predicting vs Classifying

• Linear regression naturally predicts numbers.
• How well does it handle classification over finite target feature domains?
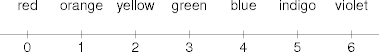
  • Map domain values into a number line.

    

• Linear regression is unbounded. What color is -1? Or 10?

Squashing Linear Functions

• Move from the weighted linear function

  f ^w(\(I\)₁, …, \(I\)_n) = w₀ + w₁\(I\)₁ + \(\cdots\) + w_n\(I\)_n

• to the squashed weighted linear function

  f ^w(\(I\)₁, …, \(I\)_n) = f(w₀ + w₁\(I\)₁ + \(\cdots\) + w_n\(I\)_n)

• f: \(\mathbb{R} \rightarrow\) [0..1] is the activation function.

Step Activation

• The step function is a simple activation function.
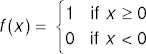
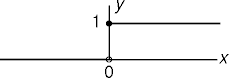
• The step function was the basis for the perceptron, the first learning method (1958).
• The step function is not differentiable, causing problems with gradient descent.

Sigmoid Activation

• The sigmoid (or logistic) function

  f(x) = 1/(1 + e-x)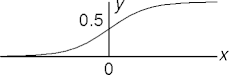

• is a differentiable activation function.
• Being differentiable, gradient descent can find minimizing weight vectors for sigmoidally squashed linear functions.

Linear Separability

• An input set of n features defines an n-dimensional space.
  • Target-feature (boolean) values are at the coordinates.
• An input set is linearly separable iff a n-1-dimensional hyperplane divides the target values into true and false sides.
• A non-boolean valued feature domain can be reduced to a set of boolean feature domains.

Example

• The input set (X, Y) with boolean features is a two-dimensional space, a plane.
• The one-dimensional hyperplane is a line.

  

Linear Separable Learning

• Sigmoidally squashed linear functions can learn linearly separable classifications to an arbitrarily small error.
  • The hyperplane “passes through” y = 0.5.
• Unfortunately, it is hard to determine if an input set is linearly separable.

To the Doctor’s Again

• Let’s go back to the doctor’s office.
• Straight probability wasn’t helpful. What about conditional probability?
• Suppose a bunch of people get sick in the same way.
  • Pr(sniffles | flu) = 0.90
  • Pr(aches | flu) = 0.85
  • Pr(spots | flu) = 0.07

Natural Categorizations

• A set of hypotheses conditioned by the same evidence is a kind of classification.
  • The evidence is the natural category (or class).
  • Hypotheses are feature values.
  • The conditional probability is the likelihood the hypothesis is a feature value.
• Given a flu category, we know how confident we can be with sniffle, ache, and spot predictions.

Bayesian Classifiers

• A Bayesian classifier exploits natural categories.
• The input and target features are part of the same natural category.
  • Once the category’s identified, determining the feature values follows the probabilities.
• But there’s a problem here. What is it?

Back in the Doctor’s Office

• There’s a patient waiting. What’s wrong?
• What do we know?
  • Pr(sniffles | flu) = 0.90
  • Pr(aches | flu) = 0.85
  • Pr(spots | flu) = 0.07
• The problem is hypothesis are evidence, and evidence is hypothesis.
  • We can see sniffles and no spots, but don’t know why.

Bayes’ Rule

• Have Pr(sniffles | flu), want Pr(flu | sniffles).
• Bayes’ rule “turns around” a conditional probability.

  Pr(h | e) = Pr(h \(\wedge\) e)/Pr(e)
  Pr(e | h) = Pr(e \(\wedge\) h)/Pr(h)
  

  Pr(h | e)Pr(e) = Pr(h \(\wedge\) e)
  Pr(e | h)Pr(h) = Pr(e \(\wedge\) h)

  Pr(e \(\wedge\) h) = Pr(h \(\wedge\) e)
  Pr(h | e)Pr(e) = Pr(e | h)Pr(h)

Example

• Given Pr(sniffles | flu), use Bayes’ rule to get

  Pr(flu | sniffles)Pr(sniffles) =
  	Pr(sniffles | flu)Pr(flu)

• Divide through by Pr(sniffles):

  Pr(flu | sniffles)=
  	Pr(sniffles | flu)Pr(flu)/Pr(sniffles)

Latent Variables

• A latent variable is an unobserved random variable.
  • Flu is the latent variable in the doctor’s office example.
• A Bayesian classifier uses Bayes’ rule to find the natural category as a latent variable.
  • And then uses the natural category to predict target-feature values using conditional probabilities.

Naive Bayesian Classifier

• A naive Bayesian classifier assumes
  1. the input features are independent of each other, and
  2. the natural category is independent of everything.

  

Naive Bayes Classification

• The classifier is defined the belief net and the probabilities

  Pr(Category) and Pr(\(I\)_j | Category)

• Given input set { \(I\)₁ = v₁, …, \(I\)_k = v_k }, find

  Pr(Category | \(I\)1, …, \(I\)k) =
  	\(\prod\) Pr(\(I\)i | Category)Pr(Category)

  then predict target-feature values.

Finding Priors

• The prior probabilities Pr(Category) and Pr(\(I\)_j | Category) can be calculated from the training examples:

  Pr(Category = t_i) = n_i/\(\sum\)_j n_j
  Pr(Category = t_i | \(I\) = i_j) = n_ij/\(\sum\)_k n_kj

• where

  n_i is the t_i count.
  n_jk is the count of i_j under t_k.

Summary

• Decision trees classify target features.
• Liner regressions classify or predict target features.
• Bayesian classifiers use Bayes’ rule to predict categories, and then feature values.

References

• Learning in IS (Chapter 15) in Intelligent Systems by Robert Schalkoff, Jones and Bartlett, 2011.
• Learning from Examples (Chapter 18) in Artifical Intelligence, third edition, by Stuart Russell and Peter Norvig, Prentice Hall, 2010.

---

This page last modified on 2011 November 13.