Outline
- Algorithms and Programs
- Asymptotic Estimates
- A Behavior Hierarchy
A Program
- Program 1.
int find(int a[], int x)
for (int i = 0; i < |a|; i++)
if a[i] == x
return i
return -1
Another Program
- Program 2.
int find(int a[], int x)
l = 0
r = |a|
while l < r
m = (l + r)/2
if a[m] == x
return m
if a[m] <= x
l = m + 1
else
r = m
return -1
- Which program is better?
Program Analysis
- There are many programs, all different.
- Which program can be judged suitable?
- It depends on your criteria.
- Memory use, speed, message count, ...
- Start with execution time.
- Performance is usually related to other criteria.
- It takes time to use a resource.
- Program performance can be measured or estimated.
Determining Performance
- Measure execution time.
- It’s a definitive measure.
- But algorithms don’t execute; they’re not code.
- It requires implementing the algorithm.
- There are other problems too.
Problems
- Measurements are context dependent.
- Determining context accurately is difficult.
- Comparing results is hard.
- Contexts must match to be meaningful.
- Meaningful measurements are hard.
Estimated Performance Analysis
- If you don’t know, guess (or estimate).
- Ignore the details, go for the big picture.
- Estimating is simpler than measuring.
- Skillful professionals estimate well.
- Estimation is a skill to develop.
Estimation Advantages
- Estimates are more comparable then are measurements.
- The context is mostly ignored when estimating.
- Estimates are more durable than are measurements.
- Not as closely tied to hardware or software technology.
Modeling Algorithms
- Model the algorithm by counting important parts of the algorithm.
- The algorithm is reduced to a count, other details abstracted away.
- Make sure you understand what's being counted.
Sorting Example
- Model a sorting algorithm by counting
- the time it takes to sort n elements.
- Or the number of comparisons done.
- Or the number of elements moved.
Database Example
- Model a distributed-database algorithm by counting
- f(n) is the number of messages it takes to perform a
transaction.
- Or the time it takes to commit a transaction.
- Or the number of times a transaction is overtaken and aborted.
Asymptotic Estimates
- Counting can be tedious and difficult to get right.
- Rather than count, estimate the count.
- There are many ways to estimate counts.
- An upper bound on f(n)'s behavior is useful.
- It represents potential worst-case behavior.
- Other bounds are possible, but harder to find.
Upper-Bound Estimates
- An upper bound of f(n)’s behavior is a
function g(n) with the property that
C*g(n) >= f(n)
as n grows without bound for some positive constant C.
- That is, f(n) is never larger than g(n).
- It’s an asymptotic estimate because n grows without
bound.
Big-Oh Notation
- An alternative representation for f(n)'s upper bound is
O(f)
- This is only part of the story.
Asymptotic Estimate Properties
- For any f(n), f(n) = O(f).
- O(f) + O(g) is O(max(f, g)).
- Larger estimates swallow up smaller estimates.
- max(f, g) may not exist as n grows without bound.
- O(f)*O(g) = O(fg).
- The product of estimates is the estimate of the product.
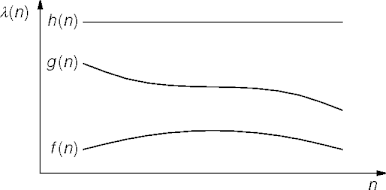
Estimate Quality
- Suppose g = O(f) and h = O(f).
Constant Behavior
- This is input-independent behavior
- This is the ideal behavior.
- But watch out for the value of C.
Logarithmic Behavior
- This is repeated dividing behavior.
Linear Behavior
- This is touch every element behavior.
Log-Linear Behavior
- This is sorting behavior.
- Repeatedly divide for every element.
Quadratic Behavior
- This is double loop behavior.
Cubic Behavior
- This is triple loop behavior.
Exponential Behavior
- This is systematic guessing behavior.
A Family Portrait
|
|
|
A Case Study
- Let n = 100.
| f | | f(n) |
|---|
| C | | C |
| log n | | 4.6 |
| n | | 100 |
| n log n | | 460.5 |
| n2 | | 10,000 |
| n3 | | 1,000,000 |
| 2n | | 1,267,650,600,228,229,401,496,703,205,376 |
- Except for small n, improving asymptotic behavior is important.
A Behavior Hierarchy
|
|
| Constant | | O(1) | | hash table searching |
| Log | | O(log n) | | binary search |
| Linear | | O(n) | | linear search |
| Log-linear | | O(n log n) | | heapsort |
| Quadratic | | O(n2) | | bubble sort |
| Cubic | | O(n3) | | matrix multiplication |
| Exponential | | O(2n) | | optimal route finding |
Summary
- Develop algorithms not programs.
- Code programs from algorithms.
- Use performance criteria to select algorithms.
- Use asymptotic estimates for performance.
|
This page last modified on 7 September 2010.
|

|