Data Structures & Algorithms
CS 305 & 503

Quiz 3, 24 November 2009

1. Explain how Shell sort generalizes one of the sorts we covered in class.

   ---

   See Lafore, page 316.

2. A colleague of yours suggests it would be easier to compute the median-of-three pivot value using the first three elements of the array segment passed to partition(). What is your opinion of your colleague’s idea?

   ---

   Using the first three values would be marginally easier than computing the mid-point index value, but it almost completely ignores the point behind using the median-of-three pivot. If the array segment is amost sorted, using three the median of three consecutive values would still leave the pivot towards one end of the segment, driving partition, and so quicksort, into worst-case behavior.

3. Suppose mergesort is modified to split the data sequence into thirds rather than halves. Give an analysis of the modified mergesort that shows the effect of the change on the algorithm's estimated running time.

   ---

   Dividing an array segment into thirds rather than halves effects mergesort’s recursive depth: rather than recursing log₂ n levels for an array with n elements, it will resurce log₃ n levels. Each level still does the same amount of O(n) work. A three-splitting mergesort does O(n log n) work.

4. Write in the proper quadrants below the names of the O(n²) worst-case sorts discussed in this section. For example, if sort algorithm X uses O(n) comparisons and O(n²) assignments during a sort, X should appear in the upper-right and lower-left quadrants. Justify your choices.

   

   ---

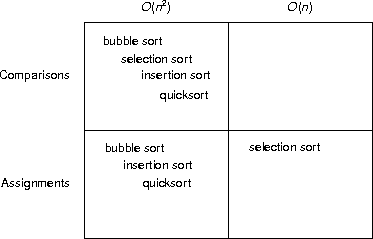
   The O(n²) sorts considered were

   • Bubble sort: repeatedly scans the unsorted section of the array, always performing O(n) comparisons per scan and, in the worst case, performing O(n) assignments. Each scan reduces the unsorted array section by one element, which results in O(n) scans. Bubble sort does O(n²) worst-case comparisons and assignments.

   • Insertion sort: repeatedly scans the sorted section of the array, performing O(n) comparisons and assignments per scan in the worst case for both operations. Each scan increases the sorted array section by one element, which results in O(n) scans. Insertion sort does O(n²) worst-case comparisons and assignments per sort.

   • Selection sort: repeatedly scans the unsorted section of the array, always performing O(n) comparisons and O(1) assignments per scan. Each scan decreases the unsorted array section by one element, which results in O(n) scans. Selection sort does O(n²) comparisons and O(n) assignments in total.

   • Quicksort: In the worst case, quicksort partitions an n-element array into 1-element and n-1-element partitions. This sequence of partitionings occurs O(n) times. Each partitioning uses, worst case, O(n) comparisons and O(n) assignments, for a total O(n²) comparisons and assignments, worst case.

     It doesn't matter how partitioning finds the pivot value: left-most, median-of-three, random choice, and so on. Each of these techniques only makes it less likely that quicksort will encounter the worst case; they don't eliminate the possibility of encountering the worst case.

   

This page last modified on 30 November 2009.