CS 306, Computer Algorithms II
Quiz 6, 25 November 2008
-
Does it make sense to use an edge list to represent a directed graph? Explain.
Not really. The edge-list representation is space efficient when representing undirected graphs because it points to the same edge for both adjacent vertices. This differs from the adjacency-list representation, which uses a separate edge for each adjacent vertex. However, a directed graph, unless it has many length two cycles, doesn't incur the redundant edge references when represented by an adjacency list, and an adjacency list has one less pointer per node overhead than does an edge list.
-
True or false: Given a connected, undirected graph with v vertices, any
subset of v edges from the graph forms a spanning tree. Justify your
answer.
Nope: Consider a graph that has a Hamiltonian circuit and let the edge subset be the edges in the circuit. The result is a cycle and not a tree.
-
Explain the conditions under which a breadth-first search over a weighted,
undirected graph would reliabiliy produce the shortest path between two
vertices.
A breadth-first search over an undirected, weighted graph produces a shortest path between two vertices when 1) all the edge weights are the same, 2) all the weights are non-negative, and 3) either of the two vertices of interest are the starting point for the search.
-
Let P be a PERT chart and L the maximally parallel task list derived
from P (that is, all tasks from P that can be done in parallel are
scheduled as parallel tasks in L). If T is scheduled in L as a
task that executes by itself, does T represent an articulation point in
P? Justify your answer. Assume that T has non-zero in and out
degrees.
It does not. The PERT chart
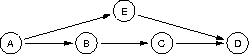
has a maximally parallel schedule [ { A }, { B, D }, { C }, { E } ], but C is not an articulation point.