CS 306, Computer Algorithms II
Quiz 4, 28 October 2008
-
A colleague of yours has a better way to delete a key from a non-self-adjusting
binary search tree: when looking for a replacement leaf: traverse the larger
(in height) of the two subtrees (if there's a choice). Your colleague's idea
is to minimize the difference in height between the two subtrees. What do you
think of your colleague's idea? Explain.
It's a so-so idea. Diving down the taller tree may take longer than diving down the shorter tree, which is a disadvantage. Deleting a leaf from the taller tree may move the two subtrees more into balance, which is an advantage, but only if there's one leaf furthest away, otherwise the height remains the same. Also, you colleague's scheme does nothing about insertions.
-
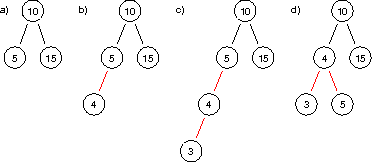
Describe an example in which a single left or right rotation is necessary and
sufficient to maintain the red-black property when inserting a key into a
red-black tree.
-
When deleting a key with at least one adjacent child from a node in an
m-way tree, m > 1, is it possible to avoid pulling up a replacement
key from a leaf of one of the key's adjacent children? Explain your answer.
Yes it is. If the key being deleted is at the end of the node's key sequence — that is, either k0 or kn-1 where n is the number of keys in the node — and the outer most child is missing — that is, either c0 or cn — then the node can be deleted without dragging up a replacement key from the other child.
-
Temporal locality is the assumption that a datum touched will be touched again
soon. Spatial locality is the assumption that a datum touched will
lead to near-by data being touched too. Is an AVL tree or a splay tree better
able to exploit spatial locality?
It depends on what you mean by “near by.” If “near by” means “children and parents” then AVL trees are better positioned than are splay trees to take advantage of spatial locality. Because they locally manipulate heights, AVL-tree rotations don't redistribute neighboring nodes too far away from the accessed node. In contrast, splay-tree rotations have potentially global effect, distributing neighboring nodes farther away from the accessed node that would an AVL tree. (Deletions from AVL trees may manipulate the tree globally too, but they are a sequence of local manipulations and not as severe in their effects as splay-tree rotations).
If “near by” means “near-by keys in order”, it seems more of a toss up. Looking at individual operations, AVL trees have the advantage by being in balance while a splay tree may be skewed past the O(log n) bound. Over a sequence of access however, which seems a more appropriate point of view relative to spatial locality, the access costs should even out.