Computer Algorithms II Lecture Notes

2 September 2008 • Introduction

Outline

• A problem and two solutions.

Three Questions

• The three questions underlying this course:

  1. How can this problem be solved?

     Algorithm design.

  2. How to represent the problem and solution?

     Data structures.

  3. How good is the solution?

     Algorithm analysis.

Number Triangles

Moves and Paths

• Number-triangle moves.

  

• Number-triangle path.

  

Path Sum

• The sum of the values along a path is the path sum.

  

• Given a number triangle, find a path with maximum sum.

What's The Solution?

• Start with the problem.

  • Given a numeric triangle.

  • Find a triangle path with maximal sum.

• Now what?

  • What does the problem say?

    • Look for paths through the triangle.

    • Keep a path with maximal sum.

Is The Algorithm Good?

• Does this work?

  • Look for paths through the triangle.

  • Keep a path with maximal sum.

• Yes, assuming

  • Path sums are computed and compared correctly.

  • All possible paths are covered.

The Algorithm

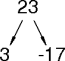
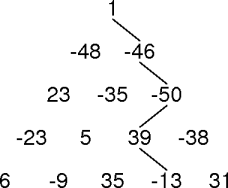
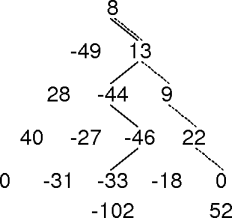
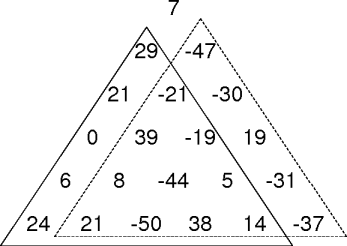
max-sum-path(triangle)

  all-paths = all-paths(triangle)
  max-path = pick(all-paths)
  max-sum = path-sum(triangle, max-path)

  for each path in all-paths
    sum = path-sum(triangle, path)
    if sum > max-sum
      max-sum = sum
      max-path = path

  return [ max-sum, max-path ]

See the code (in Scheme).

What About Data Structures?

• What's a triangle? What's a path?

  • What does the algorithm say?

    • Triangles generate paths (all-paths()).

    • Paths and triangles find sums (path-sum()).

• Don't forget the problem.

  • Triangles have numbers and are equilateral.

• Any data structures supporting this will do.

Are We Done?

• A triangle is a 2-D matrix.

• A path is a pair of arrays for rows and columns.

  • Or an array of pairs. Or...

  • A path set is an array of paths.

• path-sum() is straightforward.

• What about all-paths()?

Finding Paths

• Correctness requires all paths be considered.

• The problem allows down and to left, down and to the right.

  Is there some structure we can exploit to organize path finding?

Path Structure

• All the paths are

  • From the apex to all the paths in the left sub-triangle.

  • From the apex to all the paths in the right sub-triangle.

Path Finding

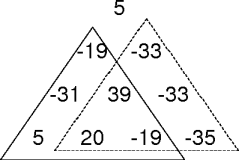
all-paths(row, col)
  if row == N
    return [ (row, col) ]

  left-paths = 
    all-paths(row + 1, col)
  right-paths = 
    all-paths(row + 1, col + 1)

  paths = []
  for path in left-paths + right-paths
    paths += (row, col) ++ path

  return paths

Is The Algorithm Good?

• How long does the algorithm take to find a solution?

  Triangle			Solution
  size			time μsec
  5			251
  10			6,270
  15			267,000
  20			8,620,000
  25			283,000,000

• It's slow. Why?

How Many Paths Are There?

• Each row requires a choice between two directions.

  • N rows leads to 2^{N - 1} possibilities.

  • This is bad.

What's The Problem?

• How many times is the middle sub-triangle searched?

• There's lots of redundant work going on.

Avoiding Repeated Work

• How can the algorithm avoid repeated work?

  • Does the work need to be repeated?

• A couple of important properties:

  1. The triangle is static; it doesn't change.

  2. A sub-triangle's max-sum path is independent of paths to the sub-triangle.

• Once the work is done, it stays done. Remember it.

Anything Else?

• There's still exponentially many paths generated.

• One final trick: there's no need to generated the paths from the top down.

  Start at the base and work towards the apex. Still wasted work, but not nearly as much as before.

Algorithm Changes

• Keep a second array to remember max-sum paths.

  • path[r,i].path is the max-sum path for the sub-triangle with apex triangle[r,i].

  • path[r,i].sum is the max-sum value for the path.

• Work from the base to the apex.

• No more path generation; no more repeated work.

A Faster Algorithm

max-sum-path(triangle)

  for i = 1 to N
    paths[N, i] = (triangle[N, i], [ (N, i) ])

  for r = N - 1 to 1
    for i = 1 to r
      path = paths[r + 1, i]
      if path.sum > paths[r + 1, i + 1].sum 
        path = paths[r + 1, i + 1]
      paths[r, i] = 
        (path.sum + triangle[r, i], 
	 (r, i) ++ path.path)

  return paths[0, 0]

Is It Faster?

Triangle			Solution Time μsec
size			All paths		Base up
5			251		434
10			6,280		1,320
15			267,000		2,330
20			8,620,000		4,050
25			283,000,000		9,080
100					167,000
500					6,750,000
1000					36,400,000